Thư Viện Bài Giảng Vật Lý Đại Cương
6.1. Các định luật cơ bản về cảm ứng điện từ
A. Lý Thuyết
1. Hiện tượng cảm ứng điện từ
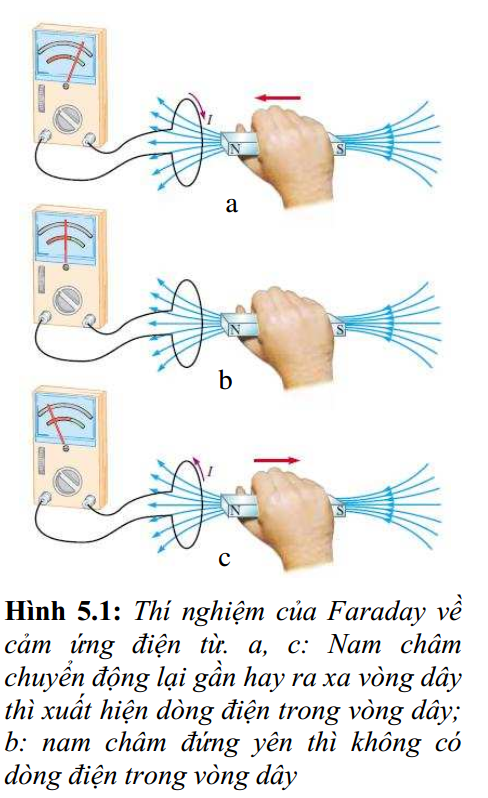
Nối hai đầu một vòng dây với một ampe kế. Đặt gần vòng dây một nam châm. Khi nam châm dịch chuyển lại gần vòng dây thì kim chỉ thị của ampe kế bị lệch đi; khi nam châm dịch chuyển ra xa vòng dây thì kim chỉ thị lệch theo chiều ngược lại; khi nam châm đứng yên thì kim chỉ thị của ampe chỉ số không (hình 5.1). Như vậy, khi nam châm chuyển động tương đối so với vòng dây thì trong vòng dây xuất hiện một dòng điện. Hiện tượng này được Faraday phát hiện ra vào năm 1831 và được gọi là hiện tượng cảm ứng điện từ.
Phân tích rất nhiều các kết quả thí nghiệm, Faraday đã đi đến kết luận rằng, mỗi khi từ thông qua một mạch kín biến thiên thì trong mạch kín xuất hiện dòng điện, gọi là dòng điện cảm ứng. Hiện tượng phát sinh ra dòng điện cảm ứng gọi là hiện tượng cảm ứng điện từ.
Nhận Dạy Kèm Vật Lý Đại Cương Online qua ứng dụng Zoom, Google Meet,...
- Dạy kèm tương tác 1 thầy 1 trò! Hỗ trợ trực tuyến 24/7
- Dạy kèm Vật Lý Đại Cương (Cơ - Nhiệt - Điện Từ - Quang - VLNT-HN)
- Bồi dưỡng HSG Vật lý các cấp, luyện thi vào lớp 10 Chuyên, ôn thi ĐH-CĐ
- Sách Giải Bài Tập Vật Lý Đại Cương - Vật Lý Kỹ Thuật - Vật Lý Lý Thuyết
- Lịch học sắp xếp linh động, sáng - chiều - tối đều học được!
- Thời gian học từ 1,5h - 2h/1 buổi!
2. Định luật Lenz
Định luật Lenz cho phép xác định chiều của dòng điện cảm ứng xuất hiện trong mạch kín bất kì khi từ thông qua mạch đó biến thiên. Nội dung của định luật Lenz được phát biểu như sau:
Dòng điện cảm ứng trong một mạch kín phải có chiều sao cho từ trường mà nó sinh ra chống lại sự biến thiên của từ thông qua mạch.

Ví dụ, để xác định chiều của dòng điện cảm ứng xuất hiện trong vòng dây ở hình 5.2, ta phân tích như sau:
Khi nam châm đi xuống thì từ thông qua vòng dây tăng lên, làm xuất hiện dòng điện cảm ứng IC trong vòng dây. Từ trường \( {{\overrightarrow{B}}_{C}} \) do dòng IC gây ra phải chống lại sự tăng của từ thông. Muốn vậy, \({{\overrightarrow{B}}_{C}}\) phải ngược chiều với từ trường \(\overrightarrow{B}\) của nam châm, nghĩa là \({{\overrightarrow{B}}_{C}}\) phải hướng lên. Dùng quy tắc đinh ốc hoặc nắm tay phải, ta xác định được dòng IC có chiều ngược chiều kim đồng hồ.
Khi nam châm chuyển động ra xa vòng dây thì từ thông qua vòng dây giảm, khi đó \({{\overrightarrow{B}}_{C}}\) cùng chiều \(\overrightarrow{B}\), kết quả dòng IC cùng chiều kim đồng hồ.
Vậy, nếu \( {{\Phi }_{m}} \) tăng thì \( {{\overrightarrow{B}}_{C}}\uparrow \downarrow \overrightarrow{B} \); nếu \( {{\Phi }_{m}} \) giảm thì \( {{\overrightarrow{B}}_{C}}\uparrow \uparrow \overrightarrow{B} \).
3. Định luật Faraday về suất điện động cảm ứng
Sự xuất hiện dòng điện cảm ứng trong mạch kín, chứng tỏ trong mạch phải tồn tại một suất điện động \( \xi \) gọi là suất điện động cảm ứng. Bằng cách phân tích các kết quả thực nghiệm của mình, Faraday đã tìm được biểu thức của suất điện động cảm ứng và phát biểu thành định luật, gọi là định luật cảm ứng điện từ:
Suất điện động cảm ứng tỉ lệ với tốc độ biến thiên của từ thông qua mạch: \( \xi =-\frac{d{{\Phi }_{m}}}{dt} \) (5.1) trong đó, \( {{\Phi }_{m}}=\int\limits_{(S)}{\overrightarrow{B}d\overrightarrow{S}} \) là từ thông qua mạch.
Nếu mạch điện có N vòng dây quấn trên một khung cứng thì: \( \xi =-N\frac{d{{\Phi }_{m}}}{dt} \) (5.2)

Trường hợp mạch điện là một vòng dây phẳng, đặt trong từ trường đều như hình 5.3 thì từ thông qua mạch là \( {{\Phi }_{m}}=BS\cos \alpha \), và do đó suất điện động trong mạch là: \( \xi =-\frac{d{{\Phi }_{m}}}{dt}=-\frac{d\left( BS\cos \alpha \right)}{dt} \) (5.3)
Nếu mạch điện là kín thì trong mạch sẽ có dòng điện I được xác định theo định luật Ohm mạch kín: \( I=\frac{\xi }{{{R}_{tm}}} \) (5.4), trong đó Rtm là điện trở của toàn mạch kín.
Nếu mạch điện là hở thì hai đầu mạch sẽ có hiệu điện thế: \( U=\left| \xi \right| \) (5.5)
Công thức (5.3) cho thấy, muốn làm xuất hiện suất điện động cảm ứng torng mạch, ta có các cách sau:
+ Thay đổi độ lớn của cảm ứng từ theo thời gian;
+ Thay đổi diện tích của mạch điện;
+ Thay đổi góc giữa pháp tuyến của mạch điện với đường sức từ;
+ Kết hợp bất kì sự thay đổi nào trong các trường hợp trên.
Dưới đây ta khảo sát vài trường hợp đặc biệt về suất điện động cảm ứng.
a) Khung dây quay đều trong từ trường đều

Quay đều khung dây với vận tốc góc \( \omega \) trong từ trường đều \( \overrightarrow{B} \) vuông góc với trục quay xx’ của khung dây (hình 5.4).
Từ thông qua khung dây là: \( \Phi =BS\cos \alpha =BS\cos \left( \omega t+\varphi \right) \) (5.6) trong đó, S là diện tích khung dây và \( \varphi \) là góc giữa \( \overrightarrow{B} \) và pháp tuyến \( \vec{n} \) của khung dây ở thời điểm t = 0.
Theo (5.2), suất điện động cảm ứng trong khung dây là: \( \xi =-N\frac{d\Phi }{dt}=NBS\omega \sin \left( \omega t+\varphi \right) \) hay \( \xi ={{\xi }_{0}}\sin \left( \omega t+\varphi \right) \) (5.6)
Trong đó: \( {{\xi }_{0}}=NBS\omega \) (5.7) là suất điện động cực đại xuất hiện trong khung dây.
Biểu thức (5.6) chứng tỏ suất điện động trong khung dây biến thiên điều hòa với tần số góc bằng tốc độ góc của khung dây.

Dựa vào nguyên tắc này, người ta chế tạo ra các máy phát điện xoay chiều. Sơ đồ cấu tạo của máy phát điện xoay chiều được minh họa trong hình 5.5. Khi khung dây quay đều trong từ trường của nam châm, hai đầu khung dây sẽ xuất hiện suất điện động biến thiên điều hòa. Để lấy điện ra mạch ngoài, người ta dùng hệ thống hai vành khuyên và hai chổi quét áp vào hai vành khuyên đó.
b) Đoạn dây dẫn chuyển động trong từ trường đều

Xét đoạn dây \( MN=\ell \) chuyển động đều với vận tốc \( \vec{v} \) trong từ trường đều \( \overrightarrow{B} \) như hình 5.6. Trong thời gian dt, đoạn MN dịch chuyển được một đoạn \( ds=vdt \); diện tích do MN quét được trong thời gian đó là \( dS=\ell .ds=\ell vdt \) và do đó, độ biến thiên của từ thông qua mạch là: \( d\Phi =BdS\cos \alpha =Bv\ell \sin \theta dt \) với \( \alpha \) là góc giữa pháp tuyến của dS với \( \overrightarrow{B} \); \( \theta \) là góc giữa \( \vec{v} \) và \( \overrightarrow{B} \).
Suy ra suất điện động xuất hiện trong mạch có độ lớn là: \( \xi =\frac{\left| d{{\Phi }_{m}} \right|}{dt}=Bv\ell \sin \theta \) (5.8)
Nếu mạch hở thì hai đầu đoạn MN có hiệu điện thế: \( U=Bv\ell \sin \theta \) (5.9)
Sự xuất hiện hiệu điện thế ở hai đầu M, N là do lực từ đã tác dụng lên các electron trong thanh MN khi nó chuyển động trong từ trường. Dùng quy tắc bàn tay phải, ta xác định được các electron trong thanh MN bị kéo về đầu N. Đầu N thừa electron nên tích điện âm, đầu M thiếu electron nên tích điện dương.
Vậy, một đoạn dây dẫn thẳng chuyển động cắt các đường sức từ thì tương đương như một nguồn điện có suất điện động tính theo (5.8). Nếu đoạn dây chuyển động vuông góc với đường cảm ứng từ thì: \( \xi =Bv\ell \) (5.10)
c) Khung dây đặt trong từ trường bith theo thời gian

Xét một khung dây dẫn phẳng, đặt trong từ trường đều \( \overrightarrow{B} \) có các đường sức từ vuông góc với mặt phẳng khung dây (hình 5.7), có độ lớn B thay đổi điều hòa theo thời gian: \( B={{B}_{0}}\cos \left( \omega t+\varphi \right) \).
Từ thông gởi qua khung dây là: \( {{\Phi }_{m}}=BS={{B}_{0}}S\cos \left( \omega t+\varphi \right) \)
Do đó, suất điện động xuất hiện trong khung dây: \( \xi =-N\frac{d{{\Phi }_{m}}}{dt}=N{{B}_{0}}S\omega \sin \left( \omega t+\varphi \right)={{\xi }_{0}}\sin \left( \omega t+\varphi \right) \) (5.11)
Trong đó: N là số vòng dây; B0 là giá trị biên độ (cực đại) của cảm ứng từ; S là diện tích khung dây; \( \omega \) là vận tốc góc của khung dây; \( \varphi \) là pha ban đầu; \( {{\xi }_{0}}=N{{B}_{0}}S\omega \) là giá trị cực đại hay giá trị biên độ của suất điện động trong khung dây.

Công thức (5.11) chứng tỏ rằng, suất điện động trong khung dây biến thiên điều hòa với tần số bằng tần số của từ trường. Dựa vào nguyên lý này, người ta chế tạo ra các thiết bị biến đổi điện áp của dòng điện xoay chiều – gọi là máy biến áp hay máy biến thế (hình 5.8). Khi nối cuộn sơ cấp sẽ có dòng điện xoay chiều. Dòng điện này phát sinh ra từ trường biến thiên điều hòa theo thời gian. Lõi thép đóng vai trò là mạch từ khép kín, do đó đường sức của từ trường sẽ xuyên qua cuộn thứ cấp, làm từ thông qua cuộn thứ cấp biến thiên điêu hòa theo thời gian. Kết quả, trong cuộn thứ cấp xuất hiện suất điện động cảm ứng biến thiên điều hòa cùng tần số với dòng điện trong cuộn sơ cấp.
B. Bài tập có hướng dẫn giải
Câu 1. Khung dây hình chữ nhật, có 100 vòng dây. Diện tích khung dây là 300 cm2. Quay đều khung dây trong từ trường đều B = 0,2 T (trục quay vuông góc với đường sức từ) sao cho trong thời gian 0,5 giây, pháp tuyến của khung dây quét được góc 90O. Viết biểu thức sóng điện từ theo thời gian t rồi suy ra giá trị của suất điện động lúc t = 2 s, biết lúc ban đầu mặt phẳng khung dây song song với đường sức từ.
Hướng dẫn giải:
Biểu thức suất điện động xuất hiện trong khung dây: \( \xi ={{\xi }_{0}}\sin \left( \omega t+\varphi \right) \)
Với tốc độ quay của khung dây: \( \omega =\frac{\theta }{t}=\frac{\frac{\pi }{4}}{0,5}=\frac{\pi }{2}\text{ }rad/s \);
Suất điện động cực đại: \({{\xi }_{0}}=NBS\omega =100.0,2.0,03.\frac{\pi }{2}=0,3\pi \text{ }V\);
Lúc t = 0, mặt phẳng khung dây song song với đường sức từ nên góc giữa pháp tuyến \( \vec{n} \) của khung dây với đường sức từ là \( \varphi =\frac{\pi }{2} \).
Vậy, biểu thức của suất điện động là: \(\xi =0,3\pi \sin \left( \frac{\pi }{2}t+\frac{\pi }{2} \right)\text{ }V\).
Giá trị của suất điện động lúc t = 2s: \(\xi =0,3\pi \sin \left( \frac{\pi }{2}.2+\frac{\pi }{2} \right)=-0,94\text{ }V\).
Câu 2. Máy bay có sải cách 12 m (khoảng cách giữa hai đầu mút A, B của hai cánh), bay theo phương ngang với vận tốc v = 1200 km/h qua vùng mà từ trường của Trái đất, B = 10–4 T, hướng thẳng đứng từ trên xuống. Tính hiệu điện thế xuất hiện ở hai đầu cánh máy bay. Đối với quan sát của phi công, cánh bên nào tích điện dương, âm?
Hướng dẫn giải:
Ta có, vận tốc \(v=1200\text{ }km/h\approx 333\text{ }m/s\).
Do đó, hiệu điện thế xuất hiện ở hai đầu cánh máy bay là:
\( U=Bv\ell ={{10}^{-4}}.333.12=0,4V \).
Dùng quy tắc bàn tay phải ta xác định được lực từ Lorentz kéo các electron trong cánh máy bay chuyển động về bên phải. Vậy, phi công sẽ quan sát thấy đầu cánh trái điện dương, còn đầu cánh phải tích điện âm.
Các bài viết cùng chủ đề!
Các Sách Giải Bài Tập - Đề Thi do Trung tâm phát hành!
Thư Viện Bài Giảng Vật Lý Đại Cương được xây dựng trên WordPress









