Thư Viện Bài Giảng Vật Lý Đại Cương
5.4. Định lí Ampère về dòng điện toàn phần
A. Lý Thuyết
1. Lưu số của vectơ cường độ từ trường
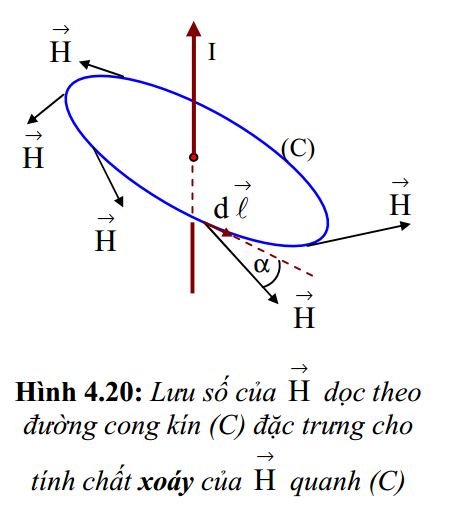
Xét một đường cong kín (C) bất kì trong không gian có từ trường. Trên (C), ta lấy một độ dời \( d\overrightarrow{\ell } \) vô cùng bé. Gọi \( \alpha \) là góc tạo bởi vectơ cường độ từ trường \( \overrightarrow{H} \) với vectơ độ dời \( d\overrightarrow{\ell } \) (hình 4.20). Tích phân \( \oint\limits_{(C)}{\overrightarrow{H}.d\overrightarrow{\ell }}=\oint\limits_{(C)}{H.d\ell .\cos \alpha } \) được gọi là lưu số (hay lưu thông) của vectơ cường độ từ trường dọc theo đường cong kín (C).
Giả sử độ lớn H không đổi dọc theo (C) thì lưu số của \( \overrightarrow{H} \) dọc theo (C) càng lớn khi \( \alpha \) càng nhỏ, nghĩa là \( \overrightarrow{H} \) càng xoáy quanh (C). Vậy, \( \oint\limits_{(C)}{\overrightarrow{H}.d\overrightarrow{\ell }} \) đặc trưng cho mức độ xoáy của \( \overrightarrow{H} \) trong diện tích giới hạn bởi (C).
Nhận Dạy Kèm Vật Lý Đại Cương Online qua ứng dụng Zoom, Google Meet,...
- Dạy kèm tương tác 1 thầy 1 trò! Hỗ trợ trực tuyến 24/7
- Dạy kèm Vật Lý Đại Cương (Cơ - Nhiệt - Điện Từ - Quang - VLNT-HN)
- Bồi dưỡng HSG Vật lý các cấp, luyện thi vào lớp 10 Chuyên, ôn thi ĐH-CĐ
- Sách Giải Bài Tập Vật Lý Đại Cương - Vật Lý Kỹ Thuật - Vật Lý Lý Thuyết
- Lịch học sắp xếp linh động, sáng - chiều - tối đều học được!
- Thời gian học từ 1,5h - 2h/1 buổi!
2. Phát biểu định lí Ampère
Lưu số của vectơ cường độ từ trường \( \overrightarrow{H} \) dọc theo một đường cong kín (C) bất kì bằng tổng đại số các dòng điện xuyên qua điện tích giới hạn bởi đường cong kín đó.
Biểu thức của định lí Ampère: \(\oint\limits_{{}}{\overrightarrow{H}d\overrightarrow{\ell }}=\sum\limits_{k=1}^{n}{{{I}_{k}}}\) (4.27)
Hay ở dạng vi phân: \( rot\overrightarrow{H}=\overrightarrow{j} \) (4.28)
Tích phân trong (4.27) là tích phân đường. Theo chiều lấy tích phân, dòng điện nào tuần theo quy tắc đinh ốc hoặc nắm tay phải sẽ có dấu dương; ngược lại là dấu âm.

Ta sẽ chứng minh (4.27) trong trường hợp đơn giản: (C) là đường cong nằm trong mặt phẳng vuông góc với dòng điện thẳng dài I, và (C) bao quanh dòng điện I (hình 4.21). Gọi \( \alpha \) là góc giữa cường độ từ trường \( \overrightarrow{H} \) và độ dời \( d\overrightarrow{\ell } \), \( d\varphi \) là góc chắn cung \( d\ell \), r là khoảng cách từ dòng điện I đến độ dời \( d\overrightarrow{\ell } \).
Ta có: \( d\ell \cos \alpha =rd\varphi \), và \( H=\frac{B}{{{\mu }_{0}}\mu }=\frac{I}{2\pi r} \).
Do đó, lưu số của vectơ \( \overrightarrow{H} \) dọc theo đường cong (C) là: \( \oint\limits_{(C)}{\overrightarrow{H}d\overrightarrow{\ell }}=\oint\limits_{(C)}{H.d\ell .\cos \alpha }=\oint\limits_{(C)}{\frac{I}{2\pi r}rd\varphi }=\frac{I}{2\pi }\int\limits_{0}^{2\pi }{d\varphi }=I \) (4.29)
Kết quả (4.29) là ta đã lấy tích phân theo chiều thuận với chiều của vectơ \( \overrightarrow{H} \). Trong trường hợp tính tích phân theo chiều ngược lại thì góc \( \alpha >{{90}^{O}} \), ta sẽ được \( \oint\limits_{(C)}{\overrightarrow{H}d\overrightarrow{\ell }}=-I \).
Nếu đường cong kín (C) không bao quanh dòng điện I thì \( \oint\limits_{(C)}{\overrightarrow{H}d\overrightarrow{\ell }}=0 \).
Trong trường hợp đường cong kín (C) bao quanh nhiều dòng điện thì theo nguyên lý chồng chất ta có, \( \overrightarrow{H}=\sum\limits_{k}{{{\overrightarrow{H}}_{k}}} \). Và do đó:
\( \oint\limits_{(C)}{\overrightarrow{H}d\overrightarrow{\ell }}=\oint\limits_{(C)}{\sum\limits_{k}{{{\overrightarrow{H}}_{k}}d\overrightarrow{\ell }}}=\sum\limits_{k}{\oint\limits_{(C)}{{{\overrightarrow{H}}_{k}}d\overrightarrow{\ell }}}=\sum\limits_{k}{{{I}_{k}}} \) (4.30)
Trong (4.30), dòng điện nào tuân theo quy tắc đinh ốc sẽ có dấu dương, trái lại là dấu âm. Định lí Ampère đã được chứng minh.
3. Vận dụng định lí Ampère để tính cường độ từ trường
Vận dụng định lí Ampère ta có thể tính cường độ từ trường của một số dòng điện có tính đối xứng, chẳng hạn như ống dây toroid, solenoid.

Xét một ống dây hình xuyến, tâm O có bán kính trong b, bán kính ngoài là c, trên đó quấn N vòng dây có dòng điện I chạy qua (xem hình 4.22).
Để tính cường độ từ trường trong lòng ống dây, ta xét một đường cong kín (C) là đường tròn tâm O, bán kính r nằm ống dây (b < r < c). Vì lí do đối xứng quanh tâm O của hình xuyến nên cường độ tụ điện tại mọi điểm trên đường cong kín (C) đều có độ lớn bằng nhau và có phương tiếp tuyến với (C). Do đó lưu số của vectơ \( \overrightarrow{H} \) dọc theo đường cong kín (C), lấy theo chiều thuận của các dòng điện là: \( \oint\limits_{(C)}{\overrightarrow{H}d\overrightarrow{\ell }}=\oint\limits_{(C)}{Hd\ell }=H\oint\limits_{(C)}{d\ell }=H.2\pi r \)
Mặt khác, tổng dòng điện xuyên qua diện tích giới hạn bởi đường cong kín (C) là: \( \sum\limits_{k=1}^{N}{{{I}_{k}}=NI} \), với N là số vòng dây quấn trên ống dây.
Theo định lí Ampère: \( \oint\limits_{(C)}{\overrightarrow{H}d\overrightarrow{\ell }}=\sum\limits_{k=1}^{N}{{{I}_{k}}} \)
Do đó, ta có: \( H.2\pi r=NI \) hay \( H=\frac{NI}{2\pi r} \) (4.31)
Kết quả (4.31) cho thấy giá trị H phụ thuộc vào r, nghĩa là từ trường trong lòng ống toroid không phải từ trường đều. Tuy nhiên, đường kính tiết diện ống toroid thường rất nhỏ, nên giá trị H thay đổi không đáng kể. Khi đó ta có: \( n=\frac{N}{2\pi r} \) (4.32) là số vòng dây trên một đơn vị chiều dài của ống dây, hay mật độ vòng dây.
Và do đó, cường độ từ trường trong lòng ống toroid là: \( H=\frac{NI}{2\pi r}=nI \) (4.33)
Bây giờ ta thứ xét xem bên ngoài ống toroid có từ trường hay không? Để trả lời cho câu hỏi đó, ta xét đường cong kín (C1) như hình 4.22. Rõ ràng, chỉ có một dòng điện duy nhất xuyên qua diện tích giới hạn bởi (C1). Theo định lí Ampère: \( \oint\limits_{({{C}_{1}})}{\overrightarrow{H}d\overrightarrow{\ell }}=\sum\limits_{k}{{{I}_{k}}}=I\ne 0 \) (4.34)
Công thức (4.34) chứng tỏ \( H\ne 0 \), nghĩa là bên ngoài ống toroid vẫn có từ trường. Tuy nhiên, cường độ từ trường bên ngoài ống toroid là rất nhỏ.
Một cách tương tự, ta cũng chứng minh được, trong lòng ống dây solenoid có từ trường đều với cường độ: \( H=\frac{NI}{\ell }=nI \) (4.35)
Các công thức (4.33) và (4.35) chứng tỏ rằng, cảm ứng từ trong lòng các ống dây điện được tính bởi: \( B={{\mu }_{0}}\mu H={{\mu }_{0}}\mu nI \) (4.36)
B. Bài tập có hướng dẫn giải
Câu 1. Tính cảm ứng từ và cường độ từ trường trong lòng ống dây solenoid, biết ống dây dài 80 cm, trên đó quấn 2000 vòng dây, cường độ dòng điện qua mỗi vòng dây là 0,5 A và hệ số từ thẩm của môi trường trong ống dây là \( \mu =500 \).
Hướng dẫn giải:
Mật độ vòng dây: \( n=\frac{N}{L}=\frac{2000}{0,8}=2500\text{ vòng/m} \)
Cường độ từ trường trong lòng ống dây: \( H=nI=2500.0,5=1250\text{ }A/m \)
Cảm ứng từ trong lòng ống dây: \( B={{\mu }_{0}}\mu H=500.4\pi {{.10}^{-7}}.1250=0,79\text{ }T \)
Các bài viết cùng chủ đề!
Các Sách Giải Bài Tập - Đề Thi do Trung tâm phát hành!
Thư Viện Bài Giảng Vật Lý Đại Cương được xây dựng trên WordPress









