3.1. Các khái niệm cơ bản của dòng điện không đổi

A. Lý Thuyết

1. Dòng điện, chiều của dòng điện

Trong môi trường dẫn, tức là môi trường có các điện tích tự do, khi không có điện trường ngoài, các hạt mang điện tự do luôn luôn chuyển động nhiệt hỗn loạn. Khi có điện trường ngoài đặt vào, dưới tác dụng của lực điện trường  \( \overrightarrow{F}=q\overrightarrow{E} \), các điện tích dương sẽ chuyển động theo chiều vectơ cường độ điện trường  \( \overrightarrow{E} \), còn các điện tích âm chuyển động ngược chiều với vectơ  \( \overrightarrow{E} \) tạo nên dòng điện.

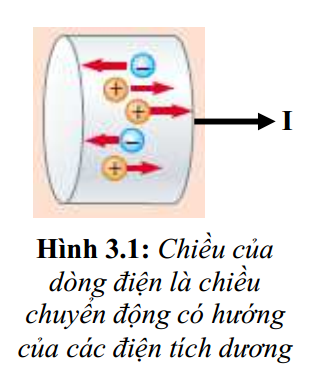
Vậy, dòng điện là dòng chuyển dời có hướng của các hạt mang điện. Chiều của dòng điện được quy ước là chiều chuyển động của các hạt mang điện dương.

Trong các môi trường dẫn khác nhau thì bản chất của dòng điện cũng khác nhau. Bản chất của dòng điện trong kim loại là dòng chuyển dời có hướng của các electron tự đo; trong chất điện phân là dòng chuyển dời có hướng của các ion dương và ion âm; trong chất khí là dòng chuyển dời có hướng của các electron, các ion dương và âm (khi chất khí bị ion hóa); trong chất bán dẫn là dòng chuyển dời có hướng của các electron và các lỗ trống.

Tuy có bản chất khác nhau, song dòng điện trong mọi môi trường luôn có các tác dụng đặc trưng cơ bản giống nhau, đó là tác dụng nhiệt, tác dụng từ, tác dụng hóa học và tác dụng sinh lí.

Nhận Dạy Kèm Vật Lý Đại Cương Online qua ứng dụng Zoom, Google Meet,...

094.625.1920 - Thầy Nhân (Zalo)

2. Cường độ dòng điện

Để định nghĩa cường độ dòng điện một cách chính xác, ta xét diện tích S vuông góc với hướng chuyển động của các điện tích như hình 3.2 (diện tích S còn gọi là tiết diện ngang). Trong thời gian  \( \Delta t  \), nếu điện lượng chuyển qua diện tích S là \( \Delta Q \) thì tỉ số:  \( I=\frac{\Delta Q}{\Delta t} \)     (3.1)  được gọi là cường độ dòng điện trung bình qua diện tích S.

Nếu xét trong thời gian  \( \Delta t  \) đủ nhỏ thì giới hạn của tỉ số  \( \frac{\Delta Q}{\Delta t} \) được gọi là cường độ dòng điện tức thời qua diện tích S.

 \( I=\underset{\Delta t\to 0}{\mathop{\lim }}\,\frac{\Delta Q}{\Delta t}=\frac{dQ}{dt} \)  (3.2)

Các công thức định nghĩa (3.1) và (3.2) chứng tỏ rằng, cường độ dòng điện là đại lượng vô hướng, bằng điện lượng chuyển qua diện tích S trong một đơn vị thời gian. Trong hệ đơn vị SI, đơn vị đo cường độ dòng điện là ampe (A) – là một trong bảy đơn vị cơ bản của hệ SI.

Đối với dòng điện có chiều không đổi, ta gọi đó là dòng điện một chiều. Đối với dòng điện có cường độ I không đổi theo thời gian thì ta gọi đó là dòng điện không đổi. Dĩ nhiên, với dòng điện không đổi thì chiều của dòng điện cũng không đổi.

Từ định nghĩa (3.2) suy ra, điện lượng  \( \Delta Q  \) chuyển qua tiết diện S trong thời gian  \( \Delta t={{t}_{2}}-{{t}_{1}} \) là:  \( \Delta Q=\int\limits_{{{t}_{1}}}^{{{t}_{2}}}{dt} \)  (3.3)

Đối với dòng điện không đổi, điện lượng  \( \Delta Q  \) chuyển qua tiết diện S trong thời gian  \( \Delta t  \) được tính bởi công thức: \(\Delta Q=I.\Delta t\) hay \(Q=It\)    (3.4)

Lưu ý, khi ta nói dòng điện I chạy qua một vật dẫn nào đó, có nghĩa là dòng điện có cường độ I chạy qua tiết diện ngang của vật dẫn đó. Chẳng hạn, nói “dòng điện 5A chạy qua bóng đèn”, có nghĩa là dòng điện có cường độ I = 5 A chạy qua bóng đèn tiết diện ngang của dây tóc bóng đèn.

Cường độ dòng điện liên quan đến chuyển động của các hạt điện. Để tìm mối quan hệ này, ta xét dòng điện không đổi I chạy qua dây dẫn thẳng hình trụ có tiết diện ngang S (hình 3.3).

Trong thời gian  \( \Delta t  \), số hạt mang điện N chuyển qua tiết diện S phải nằm trong hình trụ có chiều cao  \( \Delta x={{v}_{d}}.\Delta t  \), với vd là thành phần vận tốc của hạt điện tính dọc theo chiều của dòng điện, còn gọi là vận tốc của chuyển động có hướng của điện tích (xem hình 3.4). Gọi nO là mật độ hay nồng độ hạt tải điện của vật dẫn (tức là số hạt tải điện có trong một đơn vị thể tích của vật dẫn),  \( \Delta V  \) là thể tích của hình trụ đang xét thì  \( N={{n}_{O}}.\Delta V={{n}_{O}}S.\Delta x={{n}_{O}}S{{v}_{d}}.\Delta t  \)

Giả sử trong vật dẫn chỉ có một loại hạt tải điện thì điện lượng chuyển qua tiết diện S trong thời gian  \( \Delta t  \) là:

 \( \Delta Q=Nq={{n}_{O}}S{{v}_{d}}.\Delta t.q  \)

Do đó,cường độ dòng điện trung bình qua tiết diện S là:  \( I=\frac{\Delta Q}{\Delta t}={{n}_{O}}q{{v}_{d}}S  \)    (3.5)

Trong đó q là điện lượng của hạt điện.

3. Mật độ dòng điện

Cường độ dòng điện đặc trưng cho độ mạnh, yếu của dòng điện trên tiết diện S, mà không diễn tả được độ mạnh, yếu của dòng điện tại từng điểm trên tiết diễn S. Để đặc trưng cho dòng điện tại từng điểm trên tiết diện S, người ta đưa ra khai niệm mật độ dòng điện.

Gọi I là cường độ dòng điện qua tiết diện S đặt vuông góc với hướng chuyển động của các điện tích. Tỉ số:  \( j=\frac{I}{S} \)   (3.6) được gọi là mật độ dòng điện trung bình qua tiết diện ngang S.

Để tính mật độ dòng điện tại mỗi điểm M trong chất dẫn điện, ta xét một tiết diện ngang  \( \Delta S  \) đủ nhỏ bao quanh M và gọi  \( \Delta I  \) là cường độ dòng điện qua tiết diện  \( \Delta S  \) này thì giới hạn của tỉ số  \( \frac{\Delta I}{\Delta S} \) khi  \( \Delta S  \) tiến tới không được gọi là mật độ dòng điện tại M:  \( j=\underset{\Delta S\to 0}{\mathop{lim }}\,\frac{\Delta I}{\Delta S}=\frac{dI}{dS} \)     (3.7)

Các công thức định nghĩa (3.6) và (3.7) chứng tỏ rằng, mật độ dòng điện chính là cường độ dòng điện qua một đơn vị diện tích S đặt vuông góc với hướng chuyển động của các điện tích. Trong hệ SI, đơn vị đo mật độ dòng điện là ampe trên mét vuông (A/m2).

Kết hợp các công thức (3.6) và (3.7) với (3.5), suy ra, mật độ dòng điện j phụ thuộc vào mật độ hạt điện nO, điện lượng q của hạt điện và vận tốc của chuyển động có hướng vd của các hạt điện bởi công thức:  \( j={{n}_{O}}q{{v}_{d}} \)  (3.8) hay  dưới dạng vectơ:  \( \overrightarrow{j}={{n}_{O}}q{{\vec{v}}_{d}} \)    (3.9)

Vậy, vectơ mật độ dòng điện tại mỗi điểm tỉ lệ thuận với vectơ vận tốc chuyển động có hướng của hạt điện tại điểm đó.

Nếu biết mật độ dòng điện, ta sẽ tính được cường độ dòng điện qua tiết diện ngang S theo công thức:  \( I=\int\limits_{S}{dI}=\int\limits_{S}{jdS} \)    (3.10)

Gọi  \( \vec{n} \) là pháp vectơ đơn vị của diện tích dS và quy ước \( d\overrightarrow{S}=dS.\vec{n} \) thì ta có thể viết (3.10) dưới dạng:  \( I=\int\limits_{S}{\overrightarrow{j}.d\overrightarrow{S}}=\int\limits_{S}{j.dS.\cos \alpha } \)    (3.11)

Trong đó,  \( \alpha  \) là góc tạo bởi vectơ mật độ dòng điện  \( \overrightarrow{j} \) với pháp vectơ đơn vị  \( \vec{n} \) của diện tích S.

Công thức (3.11) có thể dùng để tính cường độ dòng điện qua một mặt cắt có diện tích S bất kì, không nhất thiết phải là tiết diện ngang.

Trường hợp mật độ dòng điện phân bố đều tại mọi điểm trên diện tích S (giá trị j không đổi tại mọi điểm), thì ta có:  \( I=j.S.\cos \alpha =j.{{S}_{n}} \)   (3.12)

Trong đó, Sn là hình chiếu của diện tích S lên phương vuông góc với vectơ mật độ dòng (Sn chính là tiết diện thẳng hay tiết diện ngang).

4. Nguồn điện, suất điện động

Xét vật A tích điện dương và vật B tích điện âm. Dùng dây dẫn, nối A với B thông qua một bóng đèn như hình 3.6. Do giữa AB có sự chênh lệch điện thế nên có dòng điện I chạy qua bóng đèn làm đèn sáng. Tuy nhiên, trong thời gian tích tắc, A và B sẽ cân bằng về điện thế và dòng điện sẽ không còn nữa.

Để duy trì dòng điện qua đèn lâu dài, ta phải giữ cho A luôn có điện thế cao hơn B. Muốn vậy, ta phải “bơm” các điện tích dương chạy ngược từ B về A. Vì lực điện trường không thể làm các điện tích dương chạy từ nơi có điện thế thấp về nơi có điện thế cao nên việc bơm các điện tích dương chạy ngược từ B trở về A được thực hiện bởi các các nguồn lực bên ngoài như lực từ, lực hóa học …. ta gọi đó là những lực “lạ”. Cơ cấu tạo ra trường lực lạ đó gọi là nguồn điện. B và A được gọi là hai cực của nguồn điện, B có điện thế thấp nên gọi là cực âm, A có điện thế cao nên gọi là cực dương.

Vậy, nguồn điện là cơ cấu tạo ra trường lực lạ để duy trì dòng điện.

Đặc trưng cho mỗi nguồn điện đó là “sức mạnh” của nguồn điện hay khả năng bơm các điện tích mạnh hay yếu, ta gọi đó là suất điện động của nguồn điện, và được định nghĩa là:  \( \xi =\frac{{{A}^{*}}}{q}=\int\limits_{B}^{A}{\overrightarrow{{{E}^{*}}}.d\overrightarrow{\ell }} \)    (3.13)

Trong đó, A* là công của trường lực lạ sinh ra khi dịch chuyển điện tích q từ B đến A;  \( \overrightarrow{{{E}^{*}}} \) là cường độ của trường lực lạ;  \( d\overrightarrow{\ell } \) là vi phân của đường đi; tích phân đường (3.13) được lấy từ cực âm đến cực dương của nguồn điện.

Vậy, suất điện động của nguồn điện là đại lượng cho khả năng sinh công của nguồn điện, đo bằng công của trường lực lạ khi dịch chuyển một đơn vị điện tích dương từ cực âm sang cực dương của nguồn điện.

Trong hệ đơn vị SI, đơn vị đo suất điện động là vôn (V), trùng với đơn vị đo điện thế, hiệu điện thế.

Khi nguồn điện làm việc, các điện tích dương sẽ được bơm từ cực âm sang cực dương, nghĩa là có dòng điện chạy qua nguồn điện. Dòng điện này sẽ làm nguồn điện nóng lên. Nói cách khác, các nguyên tử, phân tử của chất cấu tạo nên nguồn điện đã cản trở dòng điện qua nguồn điện. Như vậy, mỗi nguồn điện, ngoài suất điện động \( \xi \) đều có điện trở nội r.

Trên sơ đồ mạch điện, nguồn điện được kí hiệu như hình 3.7.

B. Bài tập có hướng dẫn giải

Câu 1. Giả sử trong mỗi giây có 2.1018 ion dương hóa trị 2 và 4.1018 electron chạy qua một đèn ống. Tính giá trị trung bình của cường độ dòng điện qua đèn. Giả sử tốc độ của các hạt diện khi dập vào các điện cực là 2.105 m/s, đường kính tiết diện của đèn ống là 2 cm. Hãy ước tính nồng độ các hạt điện.

Hướng dẫn giải:

Ta biết, mỗi electron có điện lượng  \( e=1,{{6.10}^{-19}}C  \); mỗi ion dương hóa trị 2 có điện lượng 2e. Điện lượng  \( \Delta Q  \) chuyển qua tiết diện ngang của đèn bao gồm điện lượng Q+ của các hạt ion dương và điện lượng Q– của các hạt electron. Giá trị các điện lượng này lại tỉ lệ với số hạt ion và electron tương ứng. Do đó, giá trị trung bình của cường độ dòng điện qua đèn là:

 \( I=\frac{\Delta Q}{\Delta t}=\frac{{{Q}_{+}}+{{Q}_{-}}}{\Delta t}=\frac{{{N}_{+}}.2e+{{N}_{-}}.e}{\Delta t}=\frac{\left( 2{{N}_{+}}+{{N}_{-}} \right)e}{\Delta t} \)

 \( I=\frac{\left( {{2.2.10}^{18}}+{{4.10}^{18}} \right).1,{{6.10}^{-19}}}{1}=1,28\text{ }A  \)

Gọi n1 là mật độ hạt electron và n2 là mật độ ion dương hóa trị 2 có trong bóng đèn. Các điện tích này sinh ra trong quá trình va chạm giữa các ion với nguyên tử chất khí nên thỏa mãn định luật bảo toàn điện tích.

Ta có n1 = 2n2.

Mặt khác, theo (3.5) ta có:  \( I=\left( {{n}_{1}}e+{{n}_{2}}.2e \right){{v}_{d}}S=4{{n}_{2}}e{{v}_{d}}.\pi \frac{{{d}^{2}}}{4} \)

Do đó, mật độ hạt ion dương hóa trị 2 là:

\({{n}_{2}}=\frac{I}{\pi e{{v}_{d}}.{{d}^{2}}}=\frac{1,28}{3,14.1,{{6.10}^{-19}}{{.2.10}^{5}}.0,{{02}^{2}}}=3,{{2.10}^{16}}\text{ hạt/}{{m}^{3}}\)

Mật độ hạt electron là \({{n}_{1}}=2{{n}_{2}}=6,{{4.10}^{16}}\text{ hạt/}{{m}^{3}}\).

Câu 2. Một dây chì tiết diện ngang S = 2 mm2, có dòng điện I = 5A chạy qua. Tính mật độ dòng điện qua dây chì. Dây chì này có thể chịu được dòng điện tối đa là bao nhiêu, nếu mật độ dòng cho phép là 450 A/cm2? Một động cơ có giới hạn dòng là 18A thì phải dùng dây chì có đường kính tiết diện ngang bao nhiêu để bảo vệ động cơ?

Hướng dẫn giải:

Một độ dòng điện qua dây chì: \(j=\frac{I}{S}=\frac{5\text{ }A}{2\text{ }m{{m}^{2}}}=2,5\text{ }A/m{{m}^{2}}=2,{{5.10}^{6}}\text{ }A/{{m}^{2}}\)

Dòng điện tối đa cho phép qua dây chì này:  \( {{\operatorname{I}}_{\max }}={{j}_{gh}}.S=450.0,02=9\text{ }A  \)

Nếu động cơ có giới hạn dòng Imax = 18 A thì tiết diện ngang của dây chì là:

 \( S=\frac{{{\operatorname{I}}_{\max }}}{{{j}_{gh}}}=\frac{18}{450}=0,04\text{ }c{{m}^{2}}=4\text{ }m{{m}^{2}} \)

Để bảo vệ động cơ, phải dùng dây chì có đường kính tiết diện ngang là:

\(S=\pi \frac{{{d}^{2}}}{4}\Rightarrow d=\sqrt{\frac{4S}{\pi }}=\sqrt{\frac{4.4}{3,14}}=2,26\text{ }m{{m}^{2}}\)

Các bài viết cùng chủ đề!

Hotline: 094.625.1920 - Thầy Nhân (Zalo)

Các Sách Giải Bài Tập - Đề Thi do Trung tâm phát hành!

error: Content is protected !!
MENU
Trang Chủ