Thư Viện Bài Giảng Vật Lý Đại Cương

Ở phần trên, trình bày về chất sắt từ, đã đưa ra tích phân trao đổi J_ij, đặc trưng cho năng lượng tương tác trao đổi hay xác suất trao đổi giữa các điện tử i và j của hai nguyên tử a và b trong vật thể. Đại lượng này có thể được xác định bằng biểu thức sau:  \( {{J}_{ij}}=\int{\psi _{a}^{*}(i)\psi _{b}^{*}(j)V\psi _{a}^{*}(i)\psi _{b}^{*}(j)d{{q}_{i}}d{{q}_{j}}} \)        (15.55)

Ở đây  \( \psi  và {{\psi }^{*}} \) là các hàm sóng và ánh xạ của nó, V là toán tử năng lượng tương tác giữa hai nguyên tử, q là điện tích của điện tử. Giá trị của J_ij có thể dương hoặc âm. Khi J_ij > 0 các spin định hướng song song với nhau ( \( {{\overrightarrow{S}}_{i}}\uparrow \uparrow {{\overrightarrow{S}}_{j}} \)), vật liệu là sắt từ. Khi J_ij < 0, các spin đối song song ( \( {{\overrightarrow{S}}_{i}}\uparrow \downarrow {{\overrightarrow{S}}_{j}} \)), vật liệu là phản sắt từ.

Tính chất phản sắt từ có ở nhiều vật liệu như các hợp chất MnO, MnS, MnTe, FeF₂, FeO, CoO, … các kim loại đất hiếm như Ce, Nd, Sm, Tu, … một số kim loại nhóm chuyển tiếp (nhóm sắt) như Mn, Cr.

Thực nghiệm đã chỉ ra rằng ở các nguyên tố lớp chuyển tiếp có lớp vỏ điện tử d không lấp đầy, tích phân trao đổi phụ thuộc trực tiếp vào tỉ số  \( \frac{a}{d} \), trong đó a là khoảng cách giữa các nguyên tử (hay hằng số mạng tinh thể) còn d là bán kính quỹ đạo lớp trong không lấp đầy.

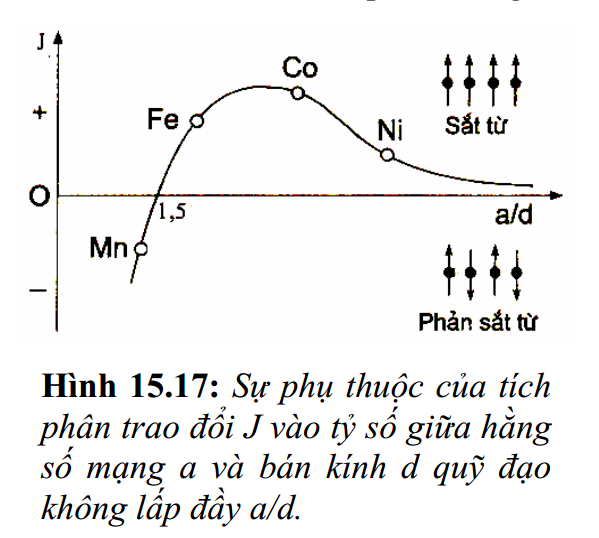
Trên hình 15.17 mô tả mối quan hệ giữa tích phân trao đổi J và tỉ số  \( \frac{a}{d} \) của các nguyên tố nhóm chuyển tiếp, ta thấy khi  \( \frac{a}{d}>1,5 \) tích phân J có giá trị dương, tương ứng với nó có các chất sắt từ Fe, Co và Ni, với  \( \frac{a}{d}<1,5 \), có J < 0, khi đó Mn, Cr, … là phản sắt từ. Bằng cách nào đó làm tăng hằng số mạng của Mn để  \( \frac{a}{d}>1,5 \) thì Mn có thể trở thành sắt từ. Thực nghiệm chứng tỏ điều này: khi pha vào Mn một lượng nhỏ nitơ sẽ làm tăng hằng số mạng của Mn và nó nhận được tính sắt từ. Nhiều hợp chất khác của Mn như MnCuAl, MnSb, MnBi,… cũng biểu thị đặc tính này.

Trong thực tế người ta có thể sử dụng phổ nhiễu xạ neutron để xác định sự sản xuất của các momen từ phản sắt từ. Hình 15.18 mô tả cấu trúc từ của MnO được xác định bằng phương pháp phổ nhiễu xạ neutron. Sự phân bố trật tự của momen từ như vậy chỉ có ở vùng nhiệt độ thấp hơn một nhiệt độ T_N, được gọi là nhiệt độ Néel.

Như vậy có thể nói vật liệu phản sắt từ tạo thành từ hai phân mạng bị từ hóa ngược chiều nhau:  \( {{M}_{A}}=-{{M}_{B}} \)     (15.16)

Các ion từ ở trong các phân mạng này không tương tác trao đổi trực tiếp với nhau mà thông qua một ion thứ 3, chẳng hạn ở MnO các ion từ Mn²⁺ tách rời nhau bởi ion không từ O^2–. Một cách tổng quát có thể coi tinh thể phản sắt từ gồm hai phân mạng sắt từ lồng vào nhau, sao cho tất cả các ion lân cận gần nhất của phân mạng thứ nhất là những ion của phân mạng thứ hai và ngược lại. Trong mỗi phân mạng các spin cùng chiều với nhau. Gọi phân mạng 1 có momen từ spin hướng lên trên, phân mạng 2 có momen từ spin hướng xuống dưới, tương ứng với chúng có các tích phân trao đổi trong mỗi phân mạng J₁₁, J₂₂ và giữa các phân mạng với nhau là J₁₂, J₂₁. Ta coi J₁₁ > 0; J₂₂ > 0; J₁₂ < 0; J₂₁ < 0. Vì hai phân mạng tương đương nên J₁₁ = J₂₂ và J₁₂ = J₂₁; đồng thời do hai nút mạng cạnh nhau thuộc hai phân mạng khác nhau nằm gần nhau hơn so với hai nút cạnh nhau thuộc cùng một phân mạng nên giả thiết  \( \left| {{J}_{12}} \right|>{{J}_{11}} \).

Theo lý thuyết trường phân tử Weiss, ta có:

\(\overrightarrow{H}_{w}^{(1)}={{\lambda }_{11}}{{\overrightarrow{M}}_{1}}+{{\lambda }_{12}}{{\overrightarrow{M}}_{2}}\) hay \(\overrightarrow{H}_{w}^{(1)}={{\lambda }_{11}}{{\overrightarrow{M}}_{1}}-\left| {{\lambda }_{12}} \right|{{\overrightarrow{M}}_{2}}\)     (15.57)

Và \(\overrightarrow{H}_{w}^{(2)}={{\lambda }_{21}}{{\overrightarrow{M}}_{1}}+{{\lambda }_{22}}{{\overrightarrow{M}}_{2}}\) hay \(\overrightarrow{H}_{w}^{(2)}=-\left| {{\lambda }_{21}} \right|{{\overrightarrow{M}}_{1}}+{{\lambda }_{22}}{{\overrightarrow{M}}_{2}}\)      (15.58)

Khi có từ trường ngoài H, mỗi phân mạng được từ hóa riêng và có độ từ hóa là:

 \( {{\overrightarrow{M}}_{1}}=\frac{{{C}_{1}}}{T}\left( \overrightarrow{H}+\overrightarrow{H}_{w}^{(1)} \right) \)        (15.59)

 \( {{\overrightarrow{M}}_{2}}=\frac{{{C}_{2}}}{T}\left( \overrightarrow{H}+\overrightarrow{H}_{w}^{(2)} \right) \)        (15.60)

Ở đây C₁, C₂ là hệ số Curie cho từng phân mạng. Vectơ độ từ hóa cho toàn phần của vật sẽ là: \(\overrightarrow{M}={{\overrightarrow{M}}_{1}}+{{\overrightarrow{M}}_{2}}=\frac{C}{2T}\left[ 2H+\left( {{\lambda }_{11}}-\left| {{\lambda }_{12}} \right| \right)M \right]\)          (15.61)

Trong này:  \( C=2{{C}_{1}}=2{{C}_{2}}=\frac{N{{g}^{2}}\mu _{B}^{2}S(S+1)}{3{{k}_{B}}} \)         (15.62)

Từ (15.61) dễ dàng rút ra biểu thức cho độ cảm từ:  \( \chi =\frac{C}{T+\theta } \)       (15.63) với  \( \theta =\frac{C}{2}\left( \left| {{\lambda }_{12}} \right|-{{\lambda }_{11}} \right) \).

Biểu thức (15.63) được coi như định luật Curie – Weiss cho chất sắt từ ở miền thuận từ (T > T_N). Ở nhiệt độ bất kỳ, M₁ và M₂ thỏa mãn các phương trình: \({{M}_{1}}={{M}_{1}}(0){{B}_{S}}\left[ \frac{g{{\mu }_{B}}S\left( H+H_{w}^{(1)} \right)}{{{k}_{B}}T} \right]\)

\({{M}_{1}}={{M}_{1}}(0){{B}_{S}}\left[ \frac{g{{\mu }_{B}}S\left( H+{{\lambda }_{11}}{{M}_{1}}-\left| {{\lambda }_{12}} \right|{{M}_{2}} \right)}{{{k}_{B}}T} \right]\)        (15.64)

\({{M}_{1}}={{M}_{2}}(0){{B}_{S}}\left[ \frac{g{{\mu }_{B}}S\left( H+H_{w}^{(2)} \right)}{{{k}_{B}}T} \right]={{M}_{2}}(0){{B}_{S}}\left[ \frac{g{{\mu }_{B}}S\left( H+{{\lambda }_{22}}{{M}_{2}}-\left| {{\lambda }_{21}} \right|{{M}_{1}} \right)}{{{k}_{B}}T} \right]\)         (15.65)

Trong đó M₁(0), M₂(0) là độ từ hóa cực đại của mỗi phân mạng ở 0 K. Giải hệ các phương trình này có thể  xác định được độ từ hóa toàn phần và độ cảm từ như là hàm của nhiệt độ đối với phản sắt từ. Kết quả tính toán cho thấy dáng điệu  \( \chi (T) \) ở T < T_N phụ thuộc vào phương của từ trường ngoài đối với phương từ hóa của hai phân mạng (hình 15.20).

Có thể xác định nhiệt độ Neel từ biểu thức sau: \({{T}_{N}}=\frac{C}{2}\left( {{\lambda }_{11}}+\left| {{\lambda }_{12}} \right| \right)=\theta \frac{{{\lambda }_{11}}+\left| {{\lambda }_{12}} \right|}{\left| {{\lambda }_{12}} \right|-{{\lambda }_{11}}}\)      (15.66)