Thư Viện Bài Giảng Vật Lý Đại Cương
3.2. Khối tâm
A. Lý Thuyết
Khi nghiên cứu chuyển động của một hệ chất điểm hay chuyển động của vật rắn, trong một số trường hợp có thể rút gọn về chuyển động của một điểm đặc trưng cho hệ đó. Điểm đặc biệt này chính là khối tâm của hệ.
1) Định nghĩa khối tâm
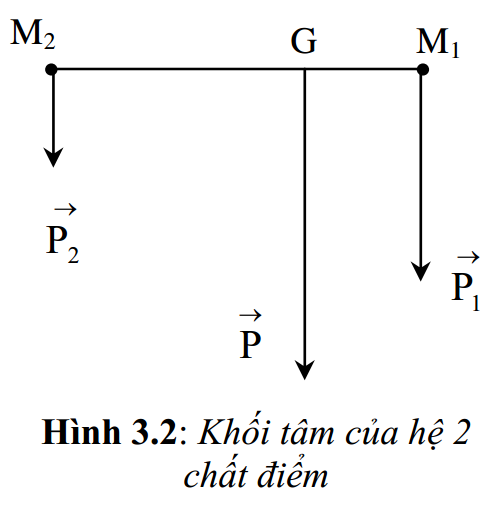
Khối được định nghĩa xuất phát từ bài toán tìm trọng tâm (điểm đặt của trọng lực) của hệ 2 chất điểm. Xét hai chất điểm M1 và M2 có khối lượng m1 và m2. Trọng lực tác dụng lên 2 chất điểm đó là \({{\overrightarrow{P}}_{1}}\) và \({{\overrightarrow{P}}_{2}}\). Hợp lực của \({{\overrightarrow{P}}_{1}}\) và \({{\overrightarrow{P}}_{2}}\) là \(\overrightarrow{P}\) có điểm đặt tại G sao cho:
\( \frac{{{M}_{1}}G}{{{M}_{2}}G}=\frac{{{P}_{2}}}{{{P}_{1}}}=\frac{{{m}_{2}}}{{{m}_{1}}} \)
\( \Rightarrow {{m}_{1}}.{{M}_{1}}G-{{m}_{2}}.{{M}_{2}}G=0 \) hay \( \Rightarrow {{m}_{1}}.\overrightarrow{{{M}_{1}}G}-{{m}_{2}}.\overrightarrow{{{M}_{2}}G}=0 \) (3.11)
Điểm G thỏa mãn (3.11) được gọi là khối tâm của hệ 2 chất điểm M1 và M2.
Trường hợp tổng quát, hệ có n chất điểm có khối lượng lần lượt là m1, m2, …, mn đặt tương ứng tại các điểm M1, M2, …, Mn, ta định nghĩa khối tâm của hệ là một điểm G thỏa mãn: \( {{m}_{1}}\overrightarrow{{{M}_{1}}G}+{{m}_{2}}\overrightarrow{{{M}_{2}}G}+…+{{m}_{n}}\overrightarrow{{{M}_{n}}G}=0 \)
Hay \( \sum\limits_{i=1}^{n}{{{m}_{i}}\overrightarrow{{{M}_{i}}G}}=0 \) (3.12)
Với vật rắn, khối tâm là điểm G thỏa mãn:
\( \int\limits_{\text{vật rắn }}{\overrightarrow{MG}dm}=\int\limits_{\text{vật rắn }}{\overrightarrow{MG}\rho dV}=0 \) (3.13)
Trong đó M là điểm bất kì trên vật rắn, dV là yếu tố thể tích bao quanh M (hình 3.1)
Khối tâm G được định nghĩa theo (3.12) và (3.13) là một điểm đặc trưng cho hệ, chỉ phụ thuộc vào vị trí tương đối theo (3.12) và (3.12) là một điểm đặc trưng cho hệ, chỉ phụ thuộc vào vị trí tương đối và phân bố khối lượng giữa các phần tử trong hệ, không phụ thuộc vào các yếu tố bên ngoài. Các kết quả tính toán cho thấy, nếu hệ có một yếu tố đối xứng (tâm đối xứng, trục đối xứng, mặt đối xứng) thì khối tâm của một hệ nằm trên yếu tố đối xứng đó. Như vậy, nếu hệ có nhiều yếu tố đối xứng thì khối tâm G thuộc về giao của các yếu tố đối xứng đó.
Ví dụ, khối tâm của đĩa tròn đồng chất, khối lượng phân bố đều chính là tâm của đĩa (giao điểm của hai đường kính); khối tâm của miếng sắt mỏng đồng chất, hình chữ nhật chính là giao điểm của 2 đường chéo, …
Cần phân biệt hai thuật ngữ “khối tâm” và “trọng tâm”! Trọng tâm G’ của hệ là điểm đặt của trọng lực tác dụng vào hệ, nghĩa là vị trí của G’ không phụ thuộc vào vị trí, khối lượng của các phần tử cấu tạo nên hệ mà còn phụ thuộc vào gia tốc trọng trường. Trong khi đó vị trí khối tâm G không phụ thuộc vào gia tốc trọng trường.
Trên thực tế, hầu hết kích thước các hệ vật lí mà ta khảo sát là không lớn, do đó gia tốc trọng trường hâu như không đổi tại mọi điểm và G’ trùng với G. Việc phân biệt vị trí của G’ và G là không cần thiết!
Nhận Dạy Kèm Vật Lý Đại Cương Online qua ứng dụng Zoom, Google Meet,...
- Dạy kèm tương tác 1 thầy 1 trò! Hỗ trợ trực tuyến 24/7
- Dạy kèm Vật Lý Đại Cương (Cơ - Nhiệt - Điện Từ - Quang - VLNT-HN)
- Sách Giải Bài Tập Vật Lý Đại Cương - Vật Lý Kỹ Thuật - Vật Lý Lý Thuyết
- Lịch học sắp xếp linh động, sáng - chiều - tối đều học được!
- Thời gian học từ 1,5h - 2h/1 buổi!
2) Tọa độ của khối rắn
Trong kỹ thuật, việc xác định chính xác khối tâm của vật rắn là hết sức quan trọng, nhất là đối với các vật rắn có chuyển động quay. Xác định khối tâm G theo định nghĩa (3.12) và (3.13) là rất phức tạp. Trong thực hành, ta có thể xác định G bằng cách tìm giao điểm của các trục đối xứng. Phương pháp này đặc biệt tiện lợi đối với các vật phẳng đồng nhất.
Trong lí thuyết, ta dùng phương pháp tọa độ. Chọn điểm O làm gốc tọa độ, vị trí của khối tâm G được xác định bởi vectơ bán kính \( {{\vec{r}}_{G}}=\overrightarrow{OG} \). Áp dụng “quy tắc 3 điểm” O, G và Mi bất kì, ta có: \( \overrightarrow{OG}={{\overrightarrow{OM}}_{i}}+\overrightarrow{{{M}_{i}}G} \).
Nhân hai về phương trình này với mi rồi lấy tổng theo i, ta có:
\( {{m}_{i}}\overrightarrow{OG}={{m}_{i}}\overrightarrow{O{{M}_{i}}}+{{m}_{i}}\overrightarrow{{{M}_{i}}G} \) và \( \sum\limits_{i=1}^{n}{{{m}_{i}}\overrightarrow{OG}}=\sum\limits_{i=1}^{n}{{{m}_{i}}\overrightarrow{O{{M}_{i}}}}+\sum\limits_{i=1}^{n}{{{m}_{i}}\overrightarrow{{{M}_{i}}G}} \)
Vì \( \overrightarrow{OG} \) không phụ thuộc vào chỉ số chạy i nên ta đưa ra ngoài dấu tổng:
\( \overrightarrow{OG}\sum\limits_{i=1}^{n}{{{m}_{i}}}=\sum\limits_{i=1}^{n}{{{m}_{i}}{{{\vec{r}}}_{i}}}+\sum\limits_{i=1}^{n}{{{m}_{i}}\overrightarrow{{{M}_{i}}G}} \)
Mà theo định nghĩa (3.12), ta có: \( \sum\limits_{i=1}^{n}{{{m}_{i}}\overrightarrow{{{M}_{i}}G}}=\vec{0} \)
Vậy: \( {{\vec{r}}_{G}}=\overrightarrow{OG}=\frac{\sum\limits_{i=1}^{n}{{{m}_{i}}{{{\vec{r}}}_{i}}}}{\sum\limits_{i=1}^{n}{{{m}_{i}}}} \) (3.14)
Trong hệ tọa độ Descartes, vectơ \( {{\vec{r}}_{i}} \) có tọa độ \( \left( {{x}_{i}};{{y}_{i}};{{z}_{i}} \right) \) nên khối tâm G của hệ có tọa độ:
\( G\left( \frac{\sum\limits_{i=1}^{n}{{{m}_{i}}{{x}_{i}}}}{\sum\limits_{i=1}^{n}{{{m}_{i}}}};\frac{\sum\limits_{i=1}^{n}{{{m}_{i}}{{y}_{i}}}}{\sum\limits_{i=1}^{n}{{{m}_{i}}}};\frac{\sum\limits_{i=1}^{n}{{{m}_{i}}{{z}_{i}}}}{\sum\limits_{i=1}^{n}{{{m}_{i}}}} \right) \) (3.15)
Với vật rắn thì tọa độ của G là: \( \left\{ \begin{align} &{{x}_{G}}=\frac{\int\limits_{\text{vật rắn}}{xdm}}{m} \\ &{{y}_{G}}=\frac{\int\limits_{\text{vật rắn}}{ydm}}{m} \\ &{{z}_{G}}=\frac{\int\limits_{\text{vật rắn }}{zdm}}{m} \\ \end{align} \right. \) (3.16)
Trong đó (x,y,z) là tọa độ của yếu tố khối lượng dm; m là khối lượng của vật rắn.
3) Chuyển động của khối tâm
Vận tốc của khối tâm:
\( {{\vec{v}}_{G}}=\frac{d{{{\vec{r}}}_{G}}}{dt}=\frac{\frac{d}{dt}\sum\limits_{i=1}^{n}{{{m}_{i}}{{{\vec{r}}}_{i}}}}{\sum\limits_{i=1}^{n}{{{m}_{i}}}}=\frac{\sum\limits_{i=1}^{n}{{{m}_{i}}\frac{d{{{\vec{r}}}_{i}}}{dt}}}{\sum\limits_{i=1}^{n}{{{m}_{i}}}}=\frac{\sum\limits_{i=1}^{n}{{{m}_{i}}{{{\vec{v}}}_{i}}}}{\sum\limits_{i=1}^{n}{{{m}_{i}}}} \) (3.20)
Tương tự, gia tốc của khối tâm: \( {{\vec{a}}_{G}}=\frac{d{{{\vec{v}}}_{G}}}{dt}=\frac{\sum\limits_{i=1}^{n}{{{m}_{i}}{{{\vec{a}}}_{i}}}}{\sum\limits_{i=1}^{n}{{{m}_{i}}}} \) (3.21)
Gọi \( {{\overrightarrow{F}}_{i}} \) và \( {{\overrightarrow{f}}_{i}} \) là tổng các ngoại lực và nội lực tác dụng lên chất điểm thứ i; \( m=\sum{{{m}_{i}}} \) là khối lượng của toàn hệ. Theo (2.6) ta có: \( {{\overrightarrow{F}}_{i}}+{{\overrightarrow{f}}_{i}}={{m}_{i}}{{\vec{a}}_{i}} \).
Suy ra: \( {{\vec{a}}_{G}}=\frac{\sum{{{\overrightarrow{F}}_{i}}+\sum{{{\overrightarrow{f}}_{i}}}}}{m} \)
Mà theo định luật III Newton, các vật trong hệ tương tác nhau bằng các lực trực đối, nên tổng các nội lực \( \sum{{{\overrightarrow{f}}_{i}}}=\vec{0} \)
Vậy: \( {{\vec{a}}_{G}}=\frac{\sum{{{\overrightarrow{F}}_{i}}}}{m} \) hay \( m{{\vec{a}}_{G}}=\sum{{{\overrightarrow{F}}_{i}}} \) (3.22)
(3.22) chính là phương trình chuyển động của khối tâm. Từ đó ta thấy rằng, khối tâm của hệ chuyển động như một chất điểm có khối lượng bằng tổng khối lượng các vật trong hệ.
Ví dụ: Khi ta ném cái rìu lên trời thì nó vừa bay, vừa xoay. Tuy vận tốc và quỹ đạo của mỗi điểm trên cái rìu là hoàn toàn khác nhau và rất phức tạp, nhưng quỹ đạo của khối tâm chắc chắn phải là đường Parabol như chuyển động ném xiên của một chất điểm (bỏ qua sức cản không khí)
B. Bài tập có hướng dẫn giải
Câu 1. Hệ ba chất điểm có khối lượng bằng nhau, đặt tại ba đỉnh của tam giác ABC. Xác định khối tâm của hệ.
Hướng dẫn giải:
Theo định nghĩa, khối tâm G thỏa: \( {{m}_{1}}\overrightarrow{AG}+{{m}_{2}}\overrightarrow{BG}+{{m}_{2}}\overrightarrow{CG}=\vec{0} \)
Vì m1 = m2 = m3 = m nên: \( \overrightarrow{AG}+\overrightarrow{BG}+\overrightarrow{CG}=\vec{0} \)
Điểm G thỏa phương trình trên chính là trọng tâm (giao điểm của ba trung tuyến) của tam giác ABC.
Câu 2. Có ba chất điểm khối lượng m1 = m2 = 2mO; m3 = 6mO đặt tại ba đỉnh A, B, C của tam giác đều, cạnh a. Xác định khối tâm G của hệ. Phải tăng hay giảm khối lượng của m3 đi bao nhiêu để khối tâm G trùng với trọng tâm \( \Delta ABC \)?
Hướng dẫn giải:

Dễ thấy, hệ đối xứng qua đường cao OC, nên G nằm trên OC. Chọn trục Ox như hình vẽ.
Theo (3.15), ta có: \( {{x}_{G}}=\frac{{{m}_{1}}{{x}_{1}}+{{m}_{2}}{{x}_{2}}+{{m}_{3}}{{x}_{3}}}{{{m}_{1}}+{{m}_{2}}+{{m}_{3}}} \)
Dể thấy: \( {{x}_{1}}={{x}_{A}}=0;{{x}_{2}}={{x}_{B}}=0;{{x}_{3}}={{x}_{C}}=\frac{\sqrt{3}}{2}a \)
Suy ra: \( {{x}_{G}}=\frac{0+0+6{{m}_{O}}.\frac{\sqrt{3}}{2}a}{10{{m}_{O}}}=\frac{3a\sqrt{3}}{10} \)
Để G trung với trọng tâm \( \Delta ABC \) thì: \( {{x}_{G}}=\frac{{{x}_{A}}+{{x}_{B}}+{{x}_{C}}}{3}=\frac{a\sqrt{3}}{6} \)
\( \Rightarrow \frac{0+0+\frac{{{m}_{3}}a\sqrt{3}}{2}}{2{{m}_{O}}+2{{m}_{O}}+{{m}_{3}}}=\frac{a\sqrt{3}}{6}\Rightarrow {{m}_{3}}=2{{m}_{O}} \)
Vậy phải giảm khối lượng vật m3 một lượng \( \Delta m=4{{m}_{O}} \)
Câu 3. Xác định khối tâm của một vật thể hình cung tròn đồng nhất, bán kính R, chắn góc ở tâm \( 2\alpha \).
Hướng dẫn giải:

Chọn trục Ox là đường phân giác của góc ở tâm như hình. Dễ thấy Ox chính là trục đối xứng của hệ. Suy ra khối tâm G phải nằm trên Ox.
Xét một yếu tố dài \( d\ell \) chắn góc ở tâm \( d\varphi \). Hoành độ của yếu tố này là: \( x=R\cos \varphi \); khối lượng chứa trong \( d\ell \) là \( dm=\lambda d\ell =\lambda Rd\varphi \). Theo (3.16), ta có:
\( {{x}_{G}}=\frac{\int\limits_{L}{xdm}}{m}=\frac{\int\limits_{L}{R\cos \varphi .\lambda Rd\varphi }}{m}=\frac{\lambda {{R}^{2}}\int\limits_{-\alpha }^{\alpha }{\cos \varphi d\varphi }}{\lambda R.2\alpha }=\frac{R\sin \alpha }{\alpha } \) (3.17)
Trong đó \( \lambda \) là mật độ khối lượng dài của cung tròn; \( m=\lambda R.2\alpha \) là khối lượng của cung tròn.
Vậy khối tâm của vật thể hình cung tròn đồng nhất nằm trên phân giác của góc ở đỉnh, các tâm một đoạn xG được xác định bởi (3.17)
Câu 4. Xác định khối tâm của một vật thể hình quạt tròn đồng nhất, bán kính R, chắn góc ở tâm \( 2\alpha \).
Hướng dẫn giải:

Tượng tự như ví dụ trước ta cũng suy ra khối tâm G của hình quạt đồng nhất nằm trên trục đối xứng Ox (đường phân giác của góc ở tâm).
Xét một yếu tố diện tích dS. Trong hệ tọa độb cực, ta có \( dS=r.dr.d\varphi \). Khối lượng chứa trong dS là \( dm=\sigma dS \); hoành độ của dS là \( x=r.\cos \varphi \). Hoành độ của khối tâm G là
\( {{x}_{G}}=\frac{\int\limits_{S}{xdm}}{m}=\frac{\iint\limits_{S}{r.\cos \varphi .\sigma dS}}{m}=\frac{\iint\limits_{S}{r.\cos \varphi .\sigma .r.dr.d\varphi }}{m} \)
\(\Rightarrow {{x}_{G}}=\frac{\sigma \int\limits_{0}^{R}{{{r}^{2}}dr}.\int\limits_{-\alpha }^{\alpha }{\cos \varphi d\varphi }}{\sigma .\alpha {{R}^{2}}}=\frac{2R\sin \alpha }{3\alpha }\)
Trong đó, \( m=\sigma .S=\sigma .\alpha {{R}^{2}} \) là khối lượng của hình quạt.
Vậy khối tâm của vật thể hình quạt đồng nhất nằm trên phân giác của góc ở đỉnh, cách tâm một đoạn xG xác định bởi (3.18).
Câu 5. Xác định khối tâm của một vật thể hình nón đồng nhất, đường cao h.
Hướng dẫn giải:
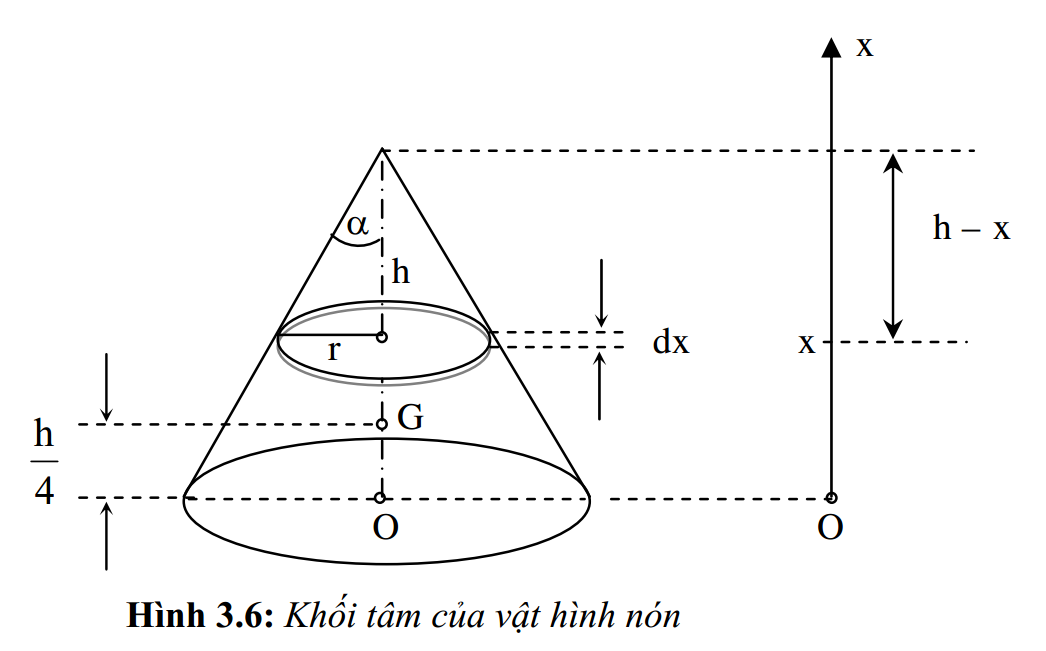
Chia hình nón thành những phần nhỏ, có dạng đĩa tròn bán kính r, bề dày dx (hình 3.6).
Ta có: \({{x}_{G}}=\frac{\int\limits_{\text{vật rắn }}{xdm}}{m}=\frac{\int\limits_{\text{vật rắn }}{x\rho dV}}{\int\limits_{\text{vật rắn }}{\rho dV}}=\frac{\int\limits_{\text{vật rắn }}{x\rho \pi {{r}^{2}}dx}}{\int\limits_{\text{vật rắn }}{\rho \pi {{r}^{2}}dx}}\)\({{x}_{G}}=\frac{\int\limits_{\text{vật rắn }}{x{{\left( h-x \right)}^{2}}.{{\tan }^{2}}\alpha .dx}}{\int\limits_{\text{vật rắn }}{{{\left( h-x \right)}^{2}}.{{\tan }^{2}}\alpha .dx}}=\frac{\int\limits_{0}^{h}{x{{\left( h-x \right)}^{2}}dx}}{\int\limits_{0}^{h}{{{\left( h-x \right)}^{2}}dx}}=\frac{h}{4}\)
Vậy, khối tâm của khối hình nón đồng nhất nằm trên trục hình nón, cách đáy một khoảng: \( {{x}_{G}}=\frac{h}{4} \) (3.19)
Các bài viết cùng chủ đề!
Các Sách Giải Bài Tập - Đề Thi do Trung tâm phát hành!
Thư Viện Bài Giảng Vật Lý Đại Cương được xây dựng trên WordPress









