Thư Viện Bài Giảng Vật Lý Đại Cương
3.4. Phương trình động lực học vật rắn
A. Lý Thuyết
1) Tổng quát
Chuyển động phức tạp của vật rắn được phân tích thành hai chuyển động đồng thời. Vì thế, mô tả chuyển động của vật rắn về mặt động lực học, ta cũng có hai phương trình:
+ Phương trình mô tả chuyển động tịnh tiến của khối tâm G:
\( \frac{d\vec{p}}{dt}=\overrightarrow{F} \) hay \( m\vec{a}=\overrightarrow{F} \) (3.38)
Với: \( \overrightarrow{F}=\sum{{{\overrightarrow{F}}_{i}}} \) là tổng các ngoại lực tác dụng lên vật rắn;
\( \vec{p}=\sum{{{m}_{i}}{{{\vec{v}}}_{i}}}=m{{\vec{v}}_{G}} \) là động lượng của vật rắn;
\( \vec{a} \) là gia tốc tịnh tiến của vật rắn (gia tốc của khối tâm).
+ Phương trình mô tả chuyển động quay quanh trục \( \Delta \) đi qua khối tâm G: \( \frac{d\overrightarrow{\mathcal{L}}}{dt}=\overrightarrow{\mathcal{M}} \) (3.39)
Với: \( \overrightarrow{\mathcal{L}}=\int\limits_{\text{vật rắn }}{d\overrightarrow{\ell }} \) là momen động lượng của vật rắn;
\( \overrightarrow{\mathcal{M}}=\sum{\left( {{{\vec{r}}}_{i}}\times {{\overrightarrow{F}}_{i}} \right)} \) là tổng momen ngoại lực đối với trục \( \Delta \)..
Hai phương trình (3,38) và (3.39) mô tả chuyển động bất kỳ của vật rắn. Nếu xét trong hệ trục Oxyz ta có 6 phương trình vi phân. Tuy nhiên, trong phạm vi chương này, ta chỉ khảo sát các chuyển động đặc biệt của vật rắn, nên việc giải các phương trình trên sẽ đợn giản hơn.
Trước hết nếu chuyển động của vật chỉ là tịnh tiến thì từ (3.38) ta thấy, chuyển động ấy được quy về chuyển động của khối tâm G và việc khảo sát giống như chuyển động của chất điểm G có khối lượng m.
Dưới đây ta sẽ khảo sát chi tiết hơn về chuyển động quay của vật rắn quanh trục cố định \( \Delta \).
Nhận Dạy Kèm Vật Lý Đại Cương Online qua ứng dụng Zoom, Google Meet,...
- Dạy kèm tương tác 1 thầy 1 trò! Hỗ trợ trực tuyến 24/7
- Dạy kèm Vật Lý Đại Cương (Cơ - Nhiệt - Điện Từ - Quang - VLNT-HN)
- Sách Giải Bài Tập Vật Lý Đại Cương - Vật Lý Kỹ Thuật - Vật Lý Lý Thuyết
- Lịch học sắp xếp linh động, sáng - chiều - tối đều học được!
- Thời gian học từ 1,5h - 2h/1 buổi!
2) Phương trình động lực học của vật rắn quay quanh trục cố định
Xét vật rắn quay quanh trục cố định \( \Delta \) với vận tốc góc \( \omega \). Theo (2.57) ta có momen động lượng của vật rắn là:
\( \overrightarrow{\mathcal{L}}=\int\limits_{\text{vật rắn }}{d\vec{\ell }}=\int\limits_{\text{vật rắn }}{dI\vec{\omega }}=\vec{\omega }\int\limits_{\text{vật rắn }}{dI}={{I}_{\Delta }}\vec{\omega } \) (3.40)
Với \(I=\int\limits_{\text{vật rắn }}{dI}=\int\limits_{\text{vật rắn }}{{{r}^{2}}dm}\) (3.41) là momen quán tính của vật rắn đối với trục quay \( \Delta \).
Chiếu (3.40) lên trục \( \Delta \), ta có: \( {{\mathcal{L}}_{\Delta }}={{I}_{\Delta }}\omega \) (3.42)
Suy ra: \( \frac{d{{\mathcal{L}}_{\Delta }}}{dt}=\frac{d\left( {{I}_{\Delta }}\omega \right)}{dt}={{I}_{\Delta }}\frac{d\omega }{dt}={{I}_{\Delta }}\beta \) (3.43)
Chiếu (3.39) lên trục \( \Delta \) và kết hợp (3.43), ta có: \( {{I}_{\Delta }}\beta ={{\mathcal{M}}_{\Delta }} \) (3.44)
(3.44) là phương trình động lực học của vật rắn quay quanh trục \( \Delta \) cố định. Trong đó: \( \beta \) là gia tốc góc, \( {{\mathcal{M}}_{\Delta }} \) là tổng đại số các momen ngoại lực đối với trục quay \( \Delta \); \( {{I}_{\Delta }} \) là momen quán tính của vật rắn đối với trục \( \Delta \). Về hình thức, (3.44) giống như phương trình cơ bản (2.6) của động lực học chất điểm, trong đó, momen quán tính I đóng vai trò giống như khối lượng m. Vì khối lượng đặc trưng cho mức quán tính nên momen quán tính cũng đặc trưng cho mức quán tính trong chuyển động quay. Do đó, người ta còn gọi momen quán tính I là quán tính quay.
Để giải được (3.44), ta cần tính được momen của các ngoại lực và momen quán tính đối với trục \( \Delta \).
3) Tính momen lực đối với trục \( \Delta \)

Để tìm hiểu rõ tác dụng làm quay vật rắn quanh trục \( \Delta \) của ngoại lực \( \overrightarrow{F} \), ta phân tích \( \overrightarrow{F} \) thành các thành phần (xem hình 3.11):
\( \overrightarrow{F}={{\overrightarrow{F}}_{//}}+{{\overrightarrow{F}}_{\bot }}={{\overrightarrow{F}}_{//}}+{{\overrightarrow{F}}_{t}}+{{\overrightarrow{F}}_{n}} \) (3.45)
+ Thành phần \( {{\overrightarrow{F}}_{//}} \) có phương song song với trục \( \Delta \), nên có tác dụng làm vật rắn trượt theo trục \( \Delta \). Thành phần này sẽ được cân bằng bởi phản lực của trục \( \Delta \).
+ Thành phần \( {{\overrightarrow{F}}_{\bot }} \) nằm trong mặt phẳng vuông góc với trục quay, lại được phân tích thành hai thành phần \( {{\overrightarrow{F}}_{t}} \) và \( {{\overrightarrow{F}}_{n}} \).
+ Thành phần \( {{\overrightarrow{F}}_{n}} \) nằm trên pháp tuyến quỹ đạo của điểm M, có tác dụng kéo vật chuyển động vuông góc với trục \( \Delta \). Thành phần này cũng được cân bằng bởi phản lực của trục quay \( \Delta \).
+ Thành phần \( {{\overrightarrow{F}}_{t}} \) hướng theo tiếp tuyến quỹ đạo của điểm M, chính thành phần này mới thực sự làm vật rắn quay quanh trục \( \Delta \).
Vậy, chỉ có thành phần tiếp tuyến của lực mới thực sự gây ra tác dụng làm quay vật rắn.

Suy ra momen của ngoại lực \( \overrightarrow{F} \) đối với trục quay \( \Delta \) (gọi tắt là momen quay) là:
\({{\overrightarrow{M}}_{\Delta }}=\overrightarrow{R}\times {{\overrightarrow{F}}_{t}}\Rightarrow {{\mathcal{M}}_{\Delta }}={{F}_{t}}.R={{F}_{\bot }}.d={{F}_{\bot }}.R\sin \theta \) (3.46)
Với R là bán kính quỹ đạo của điểm M (điểm đặt của ngoại lực); \( d=R\sin \theta \) là cánh tay đòn; \( \theta \) là góc giữa \( \overrightarrow{R} \) và thành phần \( {{\overrightarrow{F}}_{\bot }} \) (xem hình 3.12).
Từ (3.46) suy ra, momen quay sẽ lớn nhất khi lực \( \overrightarrow{F} \) nằm nằm vuông góc với trục quay và vuông góc với vectơ bán kính \( \overrightarrow{R} \).
Nếu có nhiều ngoại lực tác dụng vào vật rắn thì tổng momen của ngoại lực là: \({{\overrightarrow{\mathcal{M}}}_{\Delta }}=\sum\limits_{i}{\left( {{\overrightarrow{R}}_{i}}\times {{\overrightarrow{F}}_{ti}} \right)}\Rightarrow {{\mathcal{M}}_{\Delta }}=\sum\limits_{i}{\left( {{R}_{i}}\times {{F}_{ti}} \right)}\) (3.47)
4) Tính momen quán tính đối với trục \( \Delta \).
a) Nhắc lại các công thức định nghĩa về momen quán tính
Momen quán tính đối với trục quay \( \Delta \) của:
+ Một chất điểm: \( {{I}_{\Delta }}=m{{r}^{2}} \) (3.48)
Với r là khoảng cách từ chất điểm đến trục quay; m là khối lượng của chất điểm.
+ Hệ chất điểm: \( {{I}_{\Delta }}=\sum\limits_{i=1}^{n}{{{m}_{i}}r_{i}^{2}} \) (3.49)
Với mi là khối lượng của chất điểm thứ i; ri là khoảng cách chất điểm thứ i đến trục \( \Delta \).
+ Vật rắn: \( {{I}_{\Delta }}=\int\limits_{\text{vật rắn }}{{{r}^{2}}dm} \) (3.50)
Với r là khoảng cách từ yếu tố khối lượng dm đến trục.
Tùy theo phân bố của vật rắn mà dm có thể tính theo (3.4), (3.7) hay (3.9).
b) Momen quán tính của một số vật rắn đồng chất, khối lượng phân bố đều đối với trục quay \( \Delta \) đi qua khối tâm G.
Ví dụ 1: Tính momen quán tính của hình trụ rỗng, thành mỏng hay vành tròn đồng chất, khối lượng phân bố đều đối với trục của nó.
Hướng dẫn giải:

Chia bề mặt hình trụ làm nhiều phần, có dạng hình chữ nhật, mỗi phần có chiều rộng \( d\ell =Rd\varphi \). Gọi \( \sigma \) là mật độ khối lượng phân bố trên mặt trụ, ta có:
\(dm=\sigma dS=\sigma h.d\ell =\sigma hRd\varphi \)\(\Rightarrow dI=dm.{{R}^{2}}=\sigma h{{R}^{3}}d\varphi \)
Vì khối lượng phân bố đều nên \(\sigma =const\).
\(\Rightarrow I=\int\limits_{\text{mặt trụ }}{dI}=\int\limits_{\text{mặt trụ }}{\sigma h{{R}^{3}}d\varphi }=\sigma h{{R}^{3}}\int\limits_{0}^{2\pi }{d\varphi }\)
\(\Rightarrow I=2\pi \sigma h{{R}^{3}}=m{{R}^{3}}\)
Với \( m=2\pi \sigma hR \) là khối lượng hình trụ.
Làm tương tự đối với vành tròn (trục quay là trục của vành tròn), ta cũng có: \( I=m{{R}^{2}} \).
Vậy momen quán tính đối với trục của hình trụ rỗng, hay vành tròn đồng chất, khối lượng phân bố đều là: \( I=m{{R}^{2}} \) (3.50) với m và R là khối lượng và bán kính hình trụ hay vành tròn.
Ví dụ 2: Tính momen quán tính của khối trụ đặc hay đĩa tròn đồng chất, khối lượng phân bố đều đối với trục của nó.
Hướng dẫn giải:
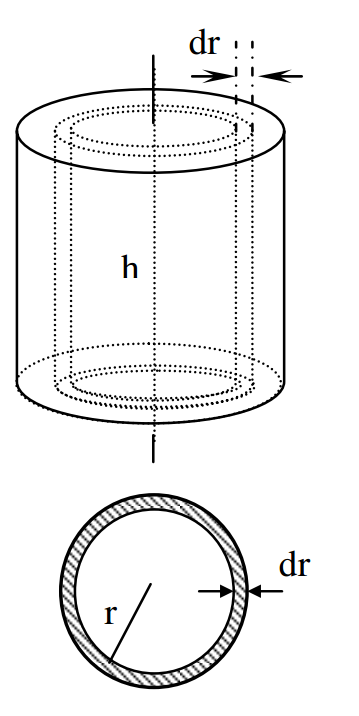
Chia khối trụ đặc thành nhiều lớp mỏng, có bề dày dr. Mỗi lớp được coi như một hình trụ rỗng, nên có momen quán tính là: \( dI=dm.{{r}^{2}}=\rho dV.{{r}^{2}} \) với \( \rho \) là khối lượng riêng của khối trụ.
Mà \(dV=dS.h=\left[ \pi {{\left( r+dr \right)}^{2}}-\pi {{r}^{2}} \right].h\approx 2\pi hrdr\)
\( \Rightarrow dI=2\pi \rho h{{r}^{3}}dr \)
\( \Rightarrow I=\int\limits_{\text{toàn khối trụ }}{dI}=2\pi\rho.h\int\limits_{0}^{R}{{{r}^{3}}dr}=\frac{1}{2}\pi \rho.h{{R}^{4}}=\frac{1}{2}m{{R}^{2}} \)
Tương tự, đối với đĩa tròn ta cũng thu được kết quả trên.
Vậy momen quán tính đối trục đối xứng của khối trụ đặc hay đĩa tròn đồng chất, khối lượng phân bố đều là: \( I=\frac{1}{2}m{{R}^{2}} \) (3.51) với m và R là khối lượng và bán kính của khối trụ hay đĩa tròn.
Ví dụ 3: Tính momen quán tính của thanh đồng chất, khối lượng m phân bố đều theo chiều dài \( \ell \) của thanh, đối với trục \( \Delta \) vuông góc với thanh.
Hướng dẫn giải:

Chia chiều dài thanh thành các phần tử nhỏ có bề dày dx. Khối lượng của mỗi phần đó là \( dm=\lambda dx \), với \( \lambda \) là mật độ khối lượng phân bố theo chiều dài của thanh. Vì khối lượng phân bố đều nên \( \lambda =const \).
Ta có: \( dI=dm.{{x}^{2}}=\lambda {{x}^{2}}dx \)
\( \Rightarrow I=\int\limits_{\text{toàn thanh }}{dI}=\lambda \int\limits_{-\frac{\ell }{2}}^{\frac{\ell }{2}}{{{x}^{2}}dx}=\frac{1}{12}\lambda {{\ell }^{3}}=\frac{1}{12}m{{\ell }^{2}} \) (3.52)
Với \( m=\lambda \ell \) là khối lượng của thanh; \( \ell \) là chiều dài của thanh.
Ví dụ 4: Tính momen quán tính của khối cầu đặc, đồng chất, khối lượng phân bố đều đối với trục quay chứa đường kính.
Hướng dẫn giải:

Momen quán tính đối với trục Oz (hình 3.17):
\( {{I}_{z}}=\int\limits_{\text{khối cầu }}{dI}=\int\limits_{\text{khối cầu }}{r_{z}^{2}dm}=\int\limits_{\text{khối cầu }}{\left( {{x}^{2}}+{{y}^{2}} \right)dm} \)
Tương tự đối với trục Ox, Oy ta cũng có:
\( {{I}_{x}}=\int\limits_{\text{khối cầu }}{\left( {{y}^{2}}+{{z}^{2}} \right)dm} \)
\( {{I}_{y}}=\int\limits_{\text{khối cầu }}{\left( {{x}^{2}}+{{z}^{2}} \right)dm} \)
Do tính đối xứng cầu nên \( {{I}_{x}}={{I}_{y}}={{I}_{z}}=I=\frac{{{I}_{x}}+{{I}_{y}}+{{I}_{z}}}{3} \)
\( \Rightarrow I=\frac{2}{3}\int\limits_{\text{khối cầu }}{\left( {{x}^{2}}+{{y}^{2}}+{{z}^{2}} \right)dm}=\frac{2}{3}\int\limits_{\text{khối cầu }}{{{r}^{2}}\rho dV} \)
Mà thể tích hình cầu là \( V=\frac{4}{3}\pi {{r}^{3}}\Rightarrow dV=4\pi {{r}^{2}}dr \)
\(\Rightarrow I=\frac{2}{3}\int\limits_{\text{khối cầu }}{{{r}^{2}}\rho .4\pi {{r}^{2}}dr}=\frac{8}{3}\pi \rho \int\limits_{0}^{R}{{{r}^{4}}dr}=\frac{8}{15}\pi \rho {{R}^{5}}=\frac{2}{5}m{{R}^{2}}\) (3.53)
Với R, \(m=\rho V=\frac{4}{3}\pi {{R}^{3}}\rho \) là bán kính, khối lượng của khối cầu.
Ví dụ 5: Tính momen quán tính của khối cầu rỗng, thành mỏng đồng chất, khối lượng phân bố đều đối với trục quay chứa đường kính.
Hướng dẫn giải:
Xét điểm M trên mặt cầu, ta có: \( {{x}^{2}}+{{y}^{2}}+{{z}^{2}}={{R}^{2}}=const \). Tương tự ví dụ 4, ta cũng có:
\( \Rightarrow I=\frac{2}{3}\int\limits_{\text{khối cầu }}{\left( {{x}^{2}}+{{y}^{2}}+{{z}^{2}} \right)dm}=\frac{2}{3}\int\limits_{\text{khối cầu }}{{{R}^{2}}dm}=\frac{2}{3}m{{R}^{2}} \) (3.54)
c) Định lí Huygens – Steiner
các công thức (3.50) đến (3.54) chỉ cho phép tính momen quán tính của vật rắn đối với trục quay \( {{\Delta }_{G}} \) đi qua khối tâm G. Trong trường hợp, trục \( \Delta \) không đi qua G nhưng song song với \( {{\Delta }_{G}} \), ta có thể vận dụng định lí Huygens – Steiner để tính:
\( {{I}_{\Delta }}={{I}_{G}}+m{{d}^{2}} \) (3.55)
Với m là khối lượng của vật rắn và d là khoảng cách giữa hai trục quay \( \Delta \) và \( {{\Delta }_{G}} \).
Chứng minh:
Xét một yếu tố khối lượng dm, các trục \( {{\Delta }_{G}} \) một đoạn x và cách trục \( \Delta \) một khoảng (x + d) (xem hình minh họa 3.18).

Momen quán tính của vật rắn đối với trục \( {{\Delta }_{G}} \) là: \( {{I}_{G}}=\int\limits_{\text{vật rắn }}{{{x}^{2}}dm} \) và đối với trục \( \Delta \) là:
\( I=\int\limits_{\text{vật rắn }}{{{\left( x+d \right)}^{2}}dm}=\int\limits_{\text{vật rắn }}{\left( {{x}^{2}}+2dx+{{d}^{2}} \right)dm} \)
\( \Rightarrow I=\int\limits_{\text{vật rắn }}{{{x}^{2}}dm}+2d\int\limits_{\text{vật rắn }}{xdm}+\int\limits_{\text{vật rắn }}{{{d}^{2}}dm} \) (*)
Số hạng thứ nhất ở vế phải của (*) chính là momen quán tính đối với trục \( {{\Delta }_{G}} \); số hạng thứ hai luôn triệt tiêu, vì hàm dưới dấu tích phân là hàm lẻ theo x và miền tính tích phân đối xứng quanh trục \( {{\Delta }_{G}} \) của vật rắn (nói cách khác nếu có yếu tố dm ở tọa độ x thì tồn tại yếu tố dm ở tọa độ ( \( -x \)) nên tích phân thứ hai bằng 0); số hạng thứ ba chính là \( m{{d}^{2}} \).
Vậy: \( {{I}_{\Delta }}={{I}_{G}}+m{{d}^{2}} \) (đpcm)
B. Bài tập có hướng dẫn giải
Câu 1.Lực F = 10 N tác dụng vào vật rắn có trục quay cố định. Biết \( \overrightarrow{F} \) nằm trong mặt phẳng vuông góc với trục quay, có điểm đặt cách trục quay 20 cm và tạo với bán kính R một góc 30O. Tính momen quay của lực.
Hướng dẫn giải:
Momen quay của lực là: \( {{\mathcal{M}}_{\Delta }}=F.R.\sin \theta =10.0,2.\sin {{30}^{O}}=1\text{ }\left( N.m \right) \)
Câu 2.Tính momen của lực để mở cánh cửa hình chữ nhật, biết lực tác dụng vào tay nắm (núm cửa) vuông góc với mặt cánh cửa, có độ lớn 5N và tay nắm ở cách bản lề 80 cm. Nếu điểm đặt của lực không phải ở núm cửa mà chỉ cách bản lề 50 cm thì độ lớn của lực phải là bao nhiêu để có momen trên?
Hướng dẫn giải:
Momen lực khi đặt tại núm cửa: MO = F.d = 5.0,8 = 4 (N.m)
Nếu điểm đặt của lực chỉ cách bản lề 50 cm thì độ lớn của lực là: \( {F}’=\frac{{{M}_{O}}}{{{d}’}}=\frac{4}{0,5}=8\text{ }N \)
Câu 3.Tính momen quán tính của thanh đồng chất đối với trục quay đi qua một đầu và vuông góc với thanh.
Hướng dẫn giải:
Áp dụng định lí Huygen – Steiner:
\( {{I}_{\Delta }}={{I}_{G}}+m{{d}^{2}}=\frac{1}{12}m{{\ell }^{2}}+m{{\left( \frac{\ell }{2} \right)}^{2}}=\frac{1}{3}m{{\ell }^{2}} \) (3.56)
Các bài viết cùng chủ đề!
Các Sách Giải Bài Tập - Đề Thi do Trung tâm phát hành!
Thư Viện Bài Giảng Vật Lý Đại Cương được xây dựng trên WordPress









