Điện thông

1. Định nghĩa

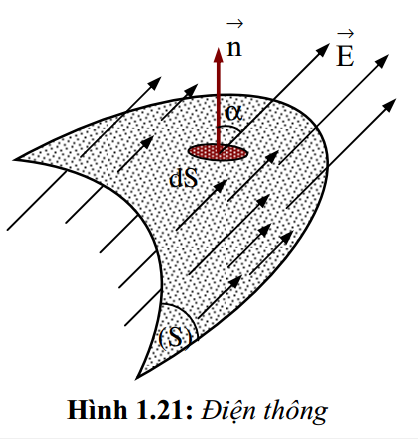
Trong không gian có điện trường, xét một bề mặt (S) bất kì, các đường sức điện trường sẽ xuyên qua mặt (S). Người ta dùng khái niệm điện thông để diễn tả số lượng đường sức điện xuyên qua mặt (S) nhiều hay ít. (hình 1.21)

Trước hết, xét một diện tích vi cấp dS đủ nhỏ của bề mặt (S) sao cho diện tích dS được coi là phẳng và cường độ điện trường tại mọi điểm trên dS là không đổi. Đại lượng vô hướng:  \( d{{\Phi }_{E}}={{E}_{n}}dS=EdS.\cos \alpha=\overrightarrow{E}.d\overrightarrow{S}\begin{matrix}   {} & (1.40)  \\\end{matrix} \)

được gọi là thông lượng điện trường hay điện thông gởi qua diện tích vi cấp dS.

Trong (1.40), E_n là hình chiếu của vectơ cường độ điện trường  \( \overrightarrow{E} \) lên pháp tuyến của dS; \(\alpha \) là góc giữa \(\overrightarrow{E}\) và pháp vectơ đơn vị \(\vec{n}\) của dS; \(d\overrightarrow{S}=dS.\vec{n}\) được gọi là vectơ điện tích.

Từ định nghĩa (1.40) suy ra, điện thông gởi qua mặt (S) bất kì là:  \( {{\Phi }_{E}}=\int\limits_{(S)}{d{{\Phi }_{E}}}=\int\limits_{(S)}{EdS\cos \alpha } \) \( =\int\limits_{(S)}{\overrightarrow{E}.\vec{n}.d\overrightarrow{S}}=\int\limits_{(S)}{\overrightarrow{E}d\overrightarrow{S}} \) (1.41)

Quy ước chọn pháp vectơ đơn vị  \( \vec{n} \) như sau: nếu mặt (S) là kín thì  \( \vec{n} \) hướng từ trong ra ngoài; nếu (S) hở thì  \( \vec{n} \) chọn tùy ý.

Ý nghĩa của điện thông: điện thông  \( {{\Phi }_{E}} \) là đại lượng vô hướng có thể âm, dương hoặc bằng không. Giá trị tuyệt đối  \( \left| {{\Phi }_{E}} \right| \) biểu diễn số đường sức điện đã xuyên qua diện tích của mặt (S).

Trong hệ SI, đơn vị đo điện thông là vôn mét (Vm).

Trường hợp đặc biệt, nếu bề mặt (S) là phẳng và điện trường là đều thì điện thông  gởi qua diện tích S là:  \( {{\Phi }_{E}}=ES\cos \alpha  \) (1.42)

2. Điện cảm, thông lượng điện cảm

Trong chất điện môi, cường độ điện trường giảm so với trong chân không. Do đó, khi đi từ chất điện môi này sang chất điện môi khác, số lượng đường sức điện sẽ thay đổi. Ta nói, đường sức điện sẽ bị gián đoạn tại bề mặt phân cách giữa hai chất điện môi. Để khắc phục điều này, người ta xây dựng vectơ điện cảm hay vectơ cảm ứng điện  \( \overrightarrow{D} \). Đối với chất điện môi đồng nhất và đẳng hướng, điện cảm  \( \overrightarrow{D} \)tại mỗi điểm tỉ lệ thuận với cường độ điện trường  \( \overrightarrow{E} \) tại điểm đó theo phương trình:

 \( \overrightarrow{D}=\varepsilon {{\varepsilon }_{0}}\overrightarrow{E}\begin{matrix}   {} & {}  \\\end{matrix} \)                 (1.43)

Trong đó:  \( \varepsilon  \) là hệ số điện môi của chất điện môi đang xét;  \( {{\varepsilon }_{0}} \) ;à hằng số điện.

(1.43) suy ra vectơ điện cảm  \( \overrightarrow{D} \) luôn song song và cùng chiều với vectơ cường độ điện trường  \( \overrightarrow{E} \). Do đó, người ta cũng xây dựng các khái niệm về đường cảm ứng điện và thông lượng cảm ứng điện.

Đường cảm ứng điện là đường mà tiếp tuyến với nó tại mỗi điểm trùng với phương của điện cảm  \( \overrightarrow{D} \), chiều của đường cảm ứng điện là chiều của điện cảm  \( \overrightarrow{D} \). Các tính chất và quy ước vẽ các đường cảm ứng điện tương tự như đường sức điện.

Thông lượng điện cảm (hay thông lượng cảm ứng điện, hay điện dịch thông) gởi qua yếu tố diện tích dS là:

 \( d{{\Phi }_{D}}={{D}_{n}}.dS=DdS\cos \alpha=\overrightarrow{D}.d\overrightarrow{S}\begin{matrix}  {} & {}  \\\end{matrix} \)                         (1.44)

Thông lượng điện cảm gởi qua mặt (S) bất kì là: \({{\Phi}_{D}}=\int\limits_{(S)}{d{{\Phi}_{D}}}=\int\limits_{(S)}{\overrightarrow{D}d\overrightarrow{S}}\begin{matrix} {} & {} \\\end{matrix} \)               (1.45)

Trong hệ SI, đơn vị đo điện cảm D là coulomb trên mét vuông (C/m²); đơn vị do thông lượng điện cảm  \( {{\Phi }_{D}} \) là coulomb (C).

Xét điện trường gây bởi một điện tích điểm Q, ta có:

 \( \overrightarrow{D}=\varepsilon {{\varepsilon }_{0}}\overrightarrow{E}=\varepsilon{{\varepsilon }_{0}}.\frac{Q}{4\pi \varepsilon {{\varepsilon}_{0}}{{r}^{2}}}.\frac{{\vec{r}}}{r}=\frac{Q}{4\pi{{r}^{2}}}.\frac{{\vec{r}}}{r}\begin{matrix}   {} & {}  \\\end{matrix} \)                 (1.46)

Công thức (1.46) chứng tỏ vectơ điện cảm  \( \overrightarrow{D} \) không phụ thuộc vào tính chất của môi trường. Do đó, các đường cảm ứng điện sẽ không bị gián đoạn tại mặt ngăn cách giữa hai chất điện môi. Điều này rất thuận tiện cho các phép tính về vi tích phân đối với vectơ  \( \overrightarrow{D} \).