Thư Viện Bài Giảng Vật Lý Đại Cương
1.4. Đường sức điện trường
A. Lý Thuyết
1.Định nghĩa
Michael Faraday, người đã đưa ra khái niệm điện trường ở thế kỉ 19, đã cho rằng không gian quanh một vật tích điện được lấp đầy bởi các đường sức. Mặc dù chúng ta không còn coi đường sức là một thực thể nữa, nhưng đường sức vẫn còn được dùng như là một cách rất hay để mô tả trực quan điện trường.
Liên hệ giữa các đường sức và các vectơ điện trường như sau: (1) Ở một điểm bất kì nào đó, hướng của một đường sức thẳng hoặc hướng của tiếp tuyến với một đường sức cong cho hướng của \( \overrightarrow{E} \) ở điểm đó và (2) các đường sức được vẽ sao cho số đường sức trên một đồng vị điện tích trong mặt phẳng thẳng góc với các đường sức tỉ lệ với độ lớn của \( \overrightarrow{E} \). Điều sau có nghĩa là ở nơi các đường súc sít nhau E lớn còn ở đâu các đường sức thưa thì E nhỏ.
Đường sức điện trường hay đường sức điện, là đường mà tiếp tuyến với nó tại mỗi điểm trùng với phương của vectơ cường độ điện trường tại điểm đó, chiều của đường sức là chiều của vectơ cường độ điện trường.

Tập hợp các đường sức điện được gọi là điện phổ. Điện phổ mô tả sự phân bố điện trường một cách trực quan.
Nhận Dạy Kèm Vật Lý Đại Cương Online qua ứng dụng Zoom, Google Meet,...
- Dạy kèm tương tác 1 thầy 1 trò! Hỗ trợ trực tuyến 24/7
- Dạy kèm Vật Lý Đại Cương (Cơ - Nhiệt - Điện Từ - Quang - VLNT-HN)
- Sách Giải Bài Tập Vật Lý Đại Cương - Vật Lý Kỹ Thuật - Vật Lý Lý Thuyết
- Lịch học sắp xếp linh động, sáng - chiều - tối đều học được!
- Thời gian học từ 1,5h - 2h/1 buổi!
2. Tính chất
+ Bất kì một điểm nào điện trường cũng vẽ được một đường sức đi qua. Thật vậy, ở điểm bất kỳ nào trong điện trường cũng có một giá trị cường độ điện trường \( \overrightarrow{E} \) xác định, nên ta vẽ được một đường sức đi qua đó.
+ Các đường sức không cắt nhau. Vì nếu chúng cắt nhau thì tại giao điểm sẽ có hai vectơ cường độ điện trường – điều này là vô lý.
+ Đường sức của điện trường tĩnh thì không khép kín, đi ra (xuất phát) từ điện tích dương, đi vào (kết thúc) ở điện tích âm.
+ Hệ đường sức điện trường đều là các đường thẳng song song cách đều nhau. Thật vậy, vì vectơ \( \overrightarrow{E} \) ở mọi điểm như nhau nên theo các tính chất 1 và 2 thì các đường sức phải song song, cùng chiều. Vì trị số \( E = const\) tại mọi điểm nên theo quy ước 3 thì mật độ đường sức như nhau ở mọi điểm, tức là các đường sức cách đều nhau.
3. Quy ước vẽ
Vẽ số đường sức điện xuyên qua một đồng vị diện tích bề mặt \( \Delta S \) (đủ nhỏ) đặt vuông góc với phương đường sức bằng với độ lớn của vectơ cường độ điện trường tại đó. (như hình 1.18)

Suy ra, nơi nào điện trường mạnh, các đường sức sẽ dày, nơi nào điện trường yếu thì đường sức sẽ thưa, nơi nào có điện trường đều thì các đường sức song song và cách đều nhau.
Số đường sức điện xuyên qua một đơn vị diện tích đặt vuông góc với phương đường sức được gọi là mật độ đường sức điện. Như vậy, vectơ cường độ điện trường tại mỗi điểm có độ lớn bằng với mật độ đường sức điện tại đó.
Hình 1.19 và 1.20 biểu diễn một số dạng đường sức của điện trường. Từ đó ta thấy ở gần các điện tích, điện trường rất mạnh.

a) Đường sức điện của điện tích điểm dương.
b) Đường sức điện của điện tích điểm âm.
c) Đường sức điện của điện trường đều.
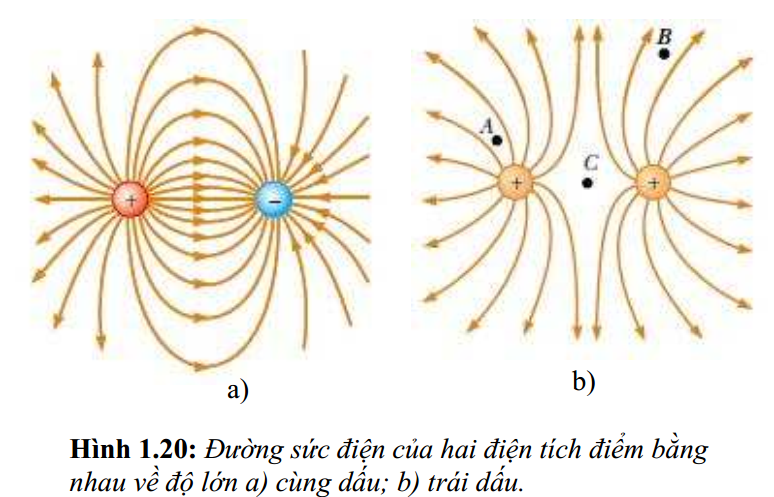
Dựa vào phân bố các đường sức tại A, B, C trong hình b) ta có thể suy ra rằng cường độ điện trường EA > EB > EC
B. Bài tập có hướng dẫn giải
Câu 1. Trong hình vẽ dưới đây, các đường sức ở bên trái có độ thưa gấp đôi độ thưa của các đường sức ở bên phải.

a) Nếu độ lớn của trường A là 40 N/C, thì lực tác dụng lên một proton ở A bằng bao nhiêu?
b) Hỏi độ lớn của trường ở B?
Hướng dẫn giải:
a) \( F=qE=1,{{6.10}^{-19}}C\times 40N/C=6,4\times {{10}^{-18}}N \).
b) Cường độ điện trường tại B bằng \( \frac{1}{2} \) cường độ điện trường tại A.
Câu 2. Vẽ định tính các đường sức ở giữa và ở ngoài 2 vỏ cầu dẫn điện đồng tâm khi vỏ trong có một điện tích q1 dương phân bố đều và vỏ ngoài có điện tích -q2 âm phân bố đều. Xét các trường hợp q1 > q2; q1 = q2 và q1 < q2.
Hướng dẫn giải:

Các bài viết cùng chủ đề!
Các Sách Giải Bài Tập - Đề Thi do Trung tâm phát hành!
Thư Viện Bài Giảng Vật Lý Đại Cương được xây dựng trên WordPress









