Thư Viện Bài Giảng Vật Lý Đại Cương

Xét điện tích điểm Q > 0, gây ra điện trường xung quanh nó. Bao quanh Q một mặt cầu (S), tâm là Q, bán kính r. Điện thông gởi qua mặt cầu này là:

 \[ {{\Phi }_{E}}=\oint\limits_{(S)}{s{{\Phi }_{E}}}=\oint\limits_{(S)}{\overrightarrow{E}d\overrightarrow{S}} \]

Do tính đối xứng cầu nên E = const tại mọi điểm trên mặt cầu và pháp vectơ đơn vị  \( \vec{n} \) của mặt (S) luôn trùng với cường độ điện trường  \( \vec{n} \) của mặt (S) luôn trùng với cường độ điện trường  \( \overrightarrow{E} \) tại mỗi điểm (hình 1.23). Do đó, điện thông gởi qua mặt cầu (S) là:

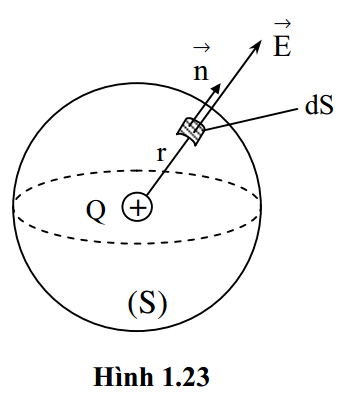
\({{\Phi }_{E}}=\oint\limits_{(S)}{EdS}=E\oint\limits_{(S)}{dS}\)\(=ES=\frac{kQ}{\varepsilon {{r}^{2}}}.4\pi {{r}^{2}}=\frac{4\pi kQ}{\varepsilon }\)

Thay  \( k=\frac{1}{4\pi {{\varepsilon }_{0}}} \), ta được:  \( {{\Phi }_{E}}=\frac{Q}{\varepsilon {{\varepsilon }_{0}}} \) (1.47)

Công thức (1.47) chứng tỏ điện thông không phụ thuộc vào bán kính r của mặt cầu. Suy ra đối với bất kì mặt cầu nào đồng tâm với (S), ví dụ (S₁), hình 1.24, ta cũng có kết quả (1.47). Điều này chứng tỏ, trong khoảng không gian giữa hai mặt cầu (S) và (S₁), nơi không có điện tích, các đường cảm ứng điện là liên tục, không bị mất đi và cũng không thêm ra. Do đó, nếu xét mặt kín (S₂) bất kì bao quanh Q thì điện thông gởi qua (S₂) cũng được tính theo (1.47).

Nếu có mặt kín (S₃) không quanh Q thì có bao nhiêu đường cảm ứng điện đi vào (S₃) thì cũng có bấy nhiêu đường cảm ứng điện đi ra khỏi (S₃) nên điện thông gởi qua (S₃) sẽ bằng không.

Kết quả (1.47) cũng đúng cho cả trường hợp bên trong mặt kín chứa nhiều điện tích, khi đó Q là tổng đại số các điện tích bên trong mặt kín. Từ đó ta có định lý Gauss hay định lí Ostrogradsky – Gauss, hay gọi tắt là định lí O – G: Điện thông gởi qua một mắt kín bất kì bằng tổng đại số các điện tích chứa trong mặt kín đó chia cho hằng số  \( {{\varepsilon }_{0}} \) và hệ số điện môi  \( \varepsilon  \).

 \( {{\Phi }_{E}}=\oint\limits_{(S)}{\overrightarrow{E}d\overrightarrow{S}}=\frac{\sum{{{Q}_{trong\text{ }(S)}}}}{\varepsilon {{\varepsilon }_{0}}} \) (1.48a)

Nhân cả hai vế của (1.48) với tích  \( \varepsilon {{\varepsilon }_{0}} \), ta được: \(\oint\limits_{(S)}{\varepsilon {{\varepsilon }_{0}}\overrightarrow{E}d\overrightarrow{S}}=\sum{{{Q}_{trong\text{ }(S)}}}\)

hay \({{\Phi }_{D}}=\oint\limits_{(S)}{\overrightarrow{D}d\overrightarrow{S}}=\sum{{{Q}_{trong\text{ }(S)}}}\) (1.48b)

và do đó, định lí Gauss còn được phát biểu là: thông lượng điện cảm gởi qua một mặt kín bất kì bằng tổng đại số các điện tích bên trong mặt kín đó.

Các công thức (1.48a) và (1.48b) được gọi là dạng tích phân của định lí Gauss. Trong trường hợp điện tích phát biểu liên tục, ta có thể biểu diễn (1.48a) và (1.48b) dưới dạng vi phân bằng các vận dụng công thức Gauss, biến một tích phân mặt thành tích phân khối:

 \( \oint\limits_{(S)}{\overrightarrow{E}.d\overrightarrow{S}}=\oint\limits_{(V)}{div\overrightarrow{E}.dV} \) (1.49)

Mặt khác, điện tích trong mặt Gauss phân bố liên tục, nên ta có:

 \( \sum{{{Q}_{trong\text{ }(S)}}=\int\limits_{(V)}{\rho .dV}} \) (1.50)

Thay (1.49) và (1.50) vào (1.48a), ta suy ra:  \( div\overrightarrow{E}=\frac{\rho }{\varepsilon {{\varepsilon }_{0}}} \) (1.51)

Tương tự, đối với điện cảm  \( \overrightarrow{D} \), ta có:  \( div\overrightarrow{D}=\rho  \) (1.52)

(1.51), (1.52) là dạng vi phân của định lí Gauss. Nó diễn tả mối quan hệ giữa cường độ điện trường  \( \overrightarrow{E} \), điện cảm  \( \overrightarrow{D} \) – là đại lượng đặc trưng cho điện trường với mật độ điện tích  \( \rho \)  – là đại lượng đặc trưng cho tính chất của môi trường tại từng điểm trong điện trường.