Thư Viện Bài Giảng Vật Lý Đại Cương
2.5. Bài toán cân bằng hệ lực phẳng với liên kết ma sát
Trong thực tế cũng như trong kỹ thuật, ma sát là một hiện tượng quan trọng nó xuất hiện khi một vật chuyển động hoặc có xu hướng chuyển động trên một vật khác. Đây là bài toán phức tạp và kết quả đạt được chủ yếu nhờ thực nghiệm.
1. Ma sát trượt
a) Thí nghiệm
Vật nặng A có trọng lượng P đặt trên mặt bàn nhám nằm ngang. Người ta buộc sợi dây vào A vắt qua ròng rọc cố định, đầu kia buộc vào một đĩa cân (Hình 2.32). Lúc đầu, đặt vào đĩa quả cân có trọng lượng Q nhỏ, Q tạo ra lực T. Khi T nhỏ, ta nhận thấy vật A vẫn đứng yên trên mặt bàn. Sở dĩ như vậy là vì mặt bàn tạo ra lực ma sát \( {{\overrightarrow{F}}_{ms}} \) ngược chiều và bằng T để cho hệ cân bằng.
Tăng T bằng cách tăng Q đến một giá trị Q* thì vật A bắt đầu mất cân bằng và vật A chuyển động trượt trên mặt bàn. Giá trị \( {{F}_{ms}} \) khi vật bắt đầu mất cân bằng gọi là \( F_{ms}^{gh} \) và ta có: \( 0\le {{F}_{ms}}\le F_{ms}^{gh}\,\,\,\,\,\,\,\,(2.5) \)
b) Phát biểu của Coulomb
Lực ma sát trượt có chiều ngược với chiều vật có xu hướng trượt và giá trị cực đại của nó tỉ lệ với phản lực pháp tuyến của mặt tựa: \( F_{ms}^{gh}=F_{ms}^{\max }=fN\,\,\,\,\,\,\,\,\,\,\,\,\,(2.6) \)
Trong đó: f gọi là hệ số ma sát, f phụ thuộc vào mặt tựa; bản chất vật liệu của mặt tựa; nhiệt độ;… Thường cho sẵn bằng bảng, f là đại lượng không thứ nguyên.
Khi vật còn cân bằng: \( {{F}_{ms}}\le fN\,\,\,\,\,\,\,\,\,(2.7) \)
Khi vật chuyển động trên mặt tựa vẫn còn lực ma sát, thường hệ số ma sát động nhỏ hơn hệ số ma sát tĩnh, tức \( {{f}_{\text{}}}<f \).
c) Phản lực toàn phần, góc ma sát
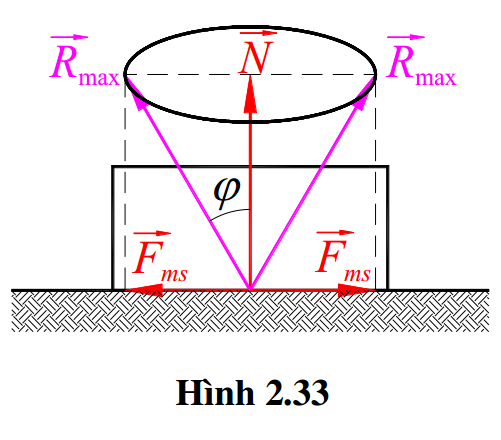
Hợp lực \( {{\overrightarrow{R}}_{ms}} \) của phản lực pháp tuyến \( \overrightarrow{N} \) và \( \overrightarrow{F_{ms}^{\max }} \) gọi là phản lực toàn phần lớn nhất. Góc \( \varphi \) tạo bởi \( \left( {{\overrightarrow{R}}_{max}},\overrightarrow{N} \right) \) gọi là góc ma sát. Khi đó nếu vật có xu hướng di chuyển theo các phia mặt tựa thì \( {{\overrightarrow{R}}_{max}} \) sẽ vẽ nên một mặt nón gọi là nón ma sát (Hình 2.33).
Nếu mặt tựa như nhau theo mọi phía thì nón ma sát là nón tròn xoay. Nhờ nón ma sát (và từng trường hợp góc ma sát) mà ta có thể xác định bài toán ma sát bằng hình học. Cụ thể khi phản lực toàn phần \( \overrightarrow{R} \) còn nằm trong nón ma sát (góc ma sát) thì vật còn cân bằng.
Chú ý: \( \tan \varphi =\frac{F_{ms}^{\max }}{N}=\frac{fN}{N}=f\,\,\,\,\,\,\,\,\,\,(2.8) \).
d) Bài toán cân bằng khi có ma sát trượt trong trường hợp vật có khả năng trượt
Ngoài các phương trình cân bằng, ta còn phải đưa vào phương trình cân bằng xác định điều kiện không trượt: (2.7) và sau đó giải như bình thường. Do trong phương trình có bất phương trình dạng (2.7) nên kết quả bài toán cân bằng khi có ma sát là một tập hợp các kết quả.
Ví dụ 1. Thanh đồng chất AB trọng lượng P, dài 2a tựa vào đầu A trên tường nhẵn thẳng đứng, còn đầu B tựa trên mặt nhẵn ngang. Biết hệ số ma sát trượt f, tìm góc \( \varphi \) bé nhất mà thanh còn cân bằng.
Nhận Dạy Kèm môn Cơ Học Kỹ Thuật (Cơ học cơ sở) - Engineering Mechanics Online qua ứng dụng Zoom, Google Meet,...
- Dạy kèm online tương tác 1 thầy 1 trò! Hỗ trợ trực tuyến 24/7
- Dạy kèm Vật Lý Kỹ Thuật gồm:
- Cơ Học Kỹ Thuật (Cơ Học Cơ Sở) - Engineering Mechanics
- Sức Bền Vật Liệu - Mechanics of Materials
- Cơ Lưu Chất - Fluid Mechanics
- Sách Giải Bài Tập của các bộ Vật Lý Đại Cương - Vật Lý Đại Cương - Vật Lý Lý Thuyết
- Bồi dưỡng ôn thi HSG các cấp - Luyện Thi vào lớp 10 khối Chuyên, Ôn Thi Đại Học môn Vật lý
- Lịch học sắp xếp sáng - chiều - tối, tất cả các buổi từ thứ 2 ➜ CN
- Thời lượng học 1,5h - 2h/1 buổi!
Hướng dẫn giải:
Xét thanh AN, ta có hệ lực cân bằng: \( \left( {{\overrightarrow{N}}_{A}},\overrightarrow{P},{{\overrightarrow{N}}_{B}},\overrightarrow{F_{ms}^{B}} \right)\sim 0 \).
Phương trình cân bằng (chọn hệ trục tọa độ Oxy):
\( \sum\limits_{k}{{{F}_{kx}}}=0\Rightarrow {{N}_{A}}-F_{ms}^{B}=0\,\,\,\,\,\,\,\,\,\,\,\,\,(1) \)
\( \sum\limits_{k}{{{F}_{ky}}}=0\Rightarrow -P+{{N}_{B}}=0\,\,\,\,\,\,\,\,\,\,\,\,\,(2) \)
\( \sum\limits_{k}{{{{\tilde{m}}}_{B}}({{\overrightarrow{F}}_{k}})}=0\Rightarrow -{{N}_{A}}\cdot AB\cdot \sin \varphi +P\cdot \frac{AB}{2}\cdot \cos \varphi =0\,\,\,\,\,\,\,\,(3) \)
Điều kiện không trượt: \( F_{ms}^{B}\le f\cdot {{N}_{B}}\,\,\,\,\,\,\,(4) \)
Giải hệ phương trình trên, ta được:
\( (2)\Rightarrow {{N}_{B}}=P;\,\,(3)\Rightarrow {{N}_{A}}=\frac{\cot \varphi }{2}P \); \( (1)\Rightarrow F_{ms}^{B}={{N}_{A}}=\frac{\cot \varphi }{2}P \)
\( (4)\Rightarrow \frac{\cot \varphi }{2}P\le f\cdot P\Rightarrow \frac{1}{\tan \varphi }\le 2f\Rightarrow \tan \varphi \ge \frac{1}{2f}\Rightarrow \varphi \ge \arctan \left( \frac{1}{2f} \right) \)
(vì \( 0\le \varphi \le \frac{\pi }{2}\Rightarrow \sin \varphi \ge 0;\,\,\cos \varphi \ge 0\Rightarrow \tan \varphi \ge 0 \))
Vậy, \( {{\varphi }_{min}}\ge \arctan \left( \frac{1}{2f} \right) \) vật còn cân bằng.
2. Ma sát lăn
a) Hiện tượng ma sát lăn
Xét một vật có khả năng lăn được (ví dụ bánh xe). Tác dụng vào trục O lực \( \overrightarrow{F} \) nằm ngang, khi lực \( \overrightarrow{F} \) còn nhỏ vật vẫn đứng yên. Tăng dần lực \( \overrightarrow{F} \) đến một giá trị F* vật bắt đầu lăn (mất cân bằng). Khi đó ngẫu lực \( \left( \overrightarrow{{{F}^{*}}},{{\overrightarrow{F}}_{max}} \right) \) cân bằng với ngẫu \( \left( \overrightarrow{P},\overrightarrow{N} \right) \) và ta có (Hình 2.36): \( R{{F}^{*}}=R{{F}_{gh}}=kN\Rightarrow {{F}_{gh}}=\frac{k}{R}N \).
Trong đó: k là hệ số ma sát lăn, có thứ nguyên [độ dài], được xác định bằng thực nghiệm.
Nếu \( F<{{F}_{gh}} \), vật cân bằng, khi \( F={{F}_{gh}} \) con lăn ở vị trí cân bằng tới hạn (bắt đầu mất cân bằng).
Định luật ma sát lăn: Ngẫu lực ma sát xuất hiện khi vật có xu hướng lăn, có chiều ngược với chiều của xu hướng lăn và có giá trị: \( {{m}_{\ell }}\le kN\,\,\,\,\,\,\,(2.9) \)
Chú ý: Đối với những vật có khả năng lăn, ma sát trượt vẫn tồn tại và thông thường hệ số ma sát lăn bé hơn nhiều lần hệ số ma sát trượt nên người ta thường bỏ qua ma sát lăn.
Sách Giải Bài Tập Cơ Học Kỹ Thuật!
b) Bài toán cân bằng khi có ma sát lăn
Ví dụ 2. Trên một đường thẳng nằm ngang có bánh xe đồng chất tâm O, bán kính R, trọng lượng P chịu tác dụng của ngẫu lực \( \tilde{m} \) và lực \( \overrightarrow{Q} \) như hình vẽ (Hình 2.37). Biết hệ số ma sát trượt f và hệ số ma sát lăn k. Xác định m và Q để bánh xe lăn không trượt.
Hướng dẫn giải:
Xét bánh xe, ta có hệ lực cân bằng: \( \left( \overrightarrow{Q},\overrightarrow{N},\overrightarrow{P},\tilde{m},{{{\tilde{m}}}_{ms}},{{\overrightarrow{F}}_{ms}} \right)\sim 0 \)
Phương trình cân bằng (chọn hệ trục tọa độ Axy):
\( \sum\limits_{k}{{{F}_{kx}}}=0\Rightarrow -Q+{{F}_{ms}}=0\,\,\,\,\,\,\,\,(1) \)
\( \sum\limits_{k}{{{F}_{ky}}}=0\Rightarrow N-P=0\,\,\,\,\,\,\,\,(2) \)
\(\sum\limits_{k}{{{{\tilde{m}}}_{A}}({{\overrightarrow{F}}_{k}})}=0\Rightarrow Q\cdot R-m+{{m}_{ms}}=0\,\,\,\,\,\,\,\,(3)\)
Điều kiện bánh xe lăn không trượt: \( \left\{ \begin{align} & {{F}_{ms}}<f\cdot N\,\,\,\,\,\,\,\,\,(4) \\ & {{m}_{ms}}=kN\,\,\,\,\,\,\,\,\,\,(5) \\ \end{align} \right. \)
Giải hệ phương trình trên, ta được:
\( (1)\Rightarrow {{F}_{ms}}=Q\,\,\,\,\,\,\,(7) \)
\( (2)\Rightarrow N=P\,\,\,\,\,\,\,\,\,\,\,\,\,(8) \)
\( (3)\Rightarrow {{m}_{ms}}=m-Q\cdot R\,\,\,\,\,\,\,\,\,\,\,\,(9) \)
Thay (7), (8), (9) vào (4) và (5) ta được: \( \left\{ \begin{align} & Q<f\cdot P \\ & m-Q\cdot R=kP \\ \end{align} \right. \)
\( \Rightarrow \left\{ \begin{align} & Q<f\cdot P \\ & m=Q\cdot R+kP \\ \end{align} \right. \) \( \Rightarrow \left\{ \begin{align}& Q<f\cdot P \\ & m<f\cdot P\cdot R+kP=(f\cdot R+k)P \\ \end{align} \right. \)
Vậy, \( \left\{ \begin{align} & Q<f\cdot P \\ & m<(f\cdot R+k)P \\ \end{align} \right. \) bánh xe lăn không trượt.
Trượt không lăn: \( \left\{ \begin{align} & {{F}_{ms}}=f\cdot N\,\,\,\,\,\,\,\,\,(10) \\ & {{m}_{ms}}<kN\,\,\,\,\,\,\,\,\,\,\,(11) \\ \end{align} \right. \)
\( \left\{ \begin{align} & Q=f\cdot P \\ & m-Q\cdot R < kP \\ \end{align} \right. \) \( \Rightarrow \left\{ \begin{align} & Q=f\cdot P \\ & m < kP+f\cdot P\cdot R=(k+f\cdot R)P \\ \end{align} \right. \)
Vậy, \( \left\{ \begin{align} & Q=f\cdot P \\ & m<(k+f\cdot R)P \\ \end{align} \right. \) bánh xe trượt không lăn.
Hãy mua Sách Giải Bài Tập Cơ Học Kỹ Thuật
Trong quá trình đăng tải bài giảng lên website sẽ không tránh khỏi việc sai sót nên để xem nhiều bài tập có lời giải chi tiết và nhiều bài toán hay hơn nữa, kính mời bạn đọc hãy mua Sách Giải Bài Tập Cơ Học Kỹ Thuật để được xem đầy đủ và chính xác nhất!
