Thư Viện Bài Giảng Vật Lý Đại Cương
1.2. Hệ tiên đề tĩnh học
1. Tiên đề 1 (tiên đề về 2 lực cân bằng)
Điều kiện cần và đủ để vật nằm cân bằng dưới tác dụng của 2 lực và 2 lực đó cùng đường tác dụng, ngược chiều nhau và cùng cường độ.
\( \left( {{\overrightarrow{F}}_{1}},{{\overrightarrow{F}}_{2}} \right)\sim 0 \)
Nhận Dạy Kèm môn Cơ Học Kỹ Thuật (Cơ học cơ sở) - Engineering Mechanics Online qua ứng dụng Zoom, Google Meet,...
- Dạy kèm online tương tác 1 thầy 1 trò! Hỗ trợ trực tuyến 24/7
- Dạy kèm Vật Lý Kỹ Thuật gồm:
- Cơ Học Kỹ Thuật (Cơ Học Cơ Sở) - Engineering Mechanics
- Sức Bền Vật Liệu - Mechanics of Materials
- Cơ Lưu Chất - Fluid Mechanics
- Sách Giải Bài Tập của các bộ Vật Lý Đại Cương - Vật Lý Đại Cương - Vật Lý Lý Thuyết
- Bồi dưỡng ôn thi HSG các cấp - Luyện Thi vào lớp 10 khối Chuyên, Ôn Thi Đại Học môn Vật lý
- Lịch học sắp xếp sáng - chiều - tối, tất cả các buổi từ thứ 2 ➜ CN
- Thời lượng học 1,5h - 2h/1 buổi!
2. Tiên đề (tiên đề về thêm bớt lực)
Tác dụng của hệ lực không thay đổi nếu thêm vào hay bớt đi một hệ lực cân bằng.
Hệ lực: \( \left( {{\overrightarrow{F}}_{1}},{{\overrightarrow{F}}_{2}},{{\overrightarrow{F}}_{3}},{{\overrightarrow{F}}_{4}},{{\overrightarrow{F}}_{5}} \right)\equiv \left( {{\overrightarrow{F}}_{1}},{{\overrightarrow{F}}_{2}},{{\overrightarrow{F}}_{3}} \right) \) nếu \( \left( {{\overrightarrow{F}}_{4}},{{\overrightarrow{F}}_{5}} \right)\equiv 0 \) (Hình 1.12)
– Hệ quả (định lý về trượt lực):
+ Tác dụng của lực lên vật rắn không thay đổi nếu ta trượt lực theo đường tác dụng của nó.
+ Chứng minh: \( \overrightarrow{F}\equiv \left( {{\overrightarrow{F}}_{1}},{{\overrightarrow{F}}_{2}},{{\overrightarrow{F}}_{3}} \right)\equiv {{\overrightarrow{F}}_{3}} \) với \( \left( {{\overrightarrow{F}}_{2}},{{\overrightarrow{F}}_{3}} \right)\equiv 0 \). Vậy vectơ lực trong tĩnh học là vectơ trượt.
3. Tiên đề 3 (Định lý về hình bình hành lực)
Hai lực tác dụng tại một điểm tương đương với 1 lực đặt tại cùng điểm đó và có vectơ lực xác định bằng đường chéo hình bình hành với các cạnh là các vectơ lực thành phần (Hình 1.14).
\( \overrightarrow{R}\simeq \left( {{\overrightarrow{F}}_{1}},{{\overrightarrow{F}}_{2}} \right) \)
4. Tiên đề 4 (tiên đề tác dụng và phản tác dụng)
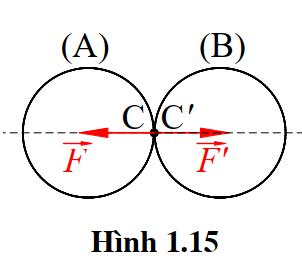
Lực tác dụng và lực phản tác dụng giữa 2 vật luôn luôn có cùng cường độ, cùng đường tác dụng và ngược chiều (Hình 1.15).
Chú ý: (B) tác dụng lực \( \overrightarrow{F} \) lên (A) tại điểm C nằm trên (A) thì (A) tác dụng lực \( \overrightarrow{{{F}’}} \) lên (B) đặt tại C’ trên (B), vì thế \( \overrightarrow{F} \) và \( \overrightarrow{{{F}’}} \) không phải là hệ lực cân bằng vì chúng không cùng nằm trên một vật rắn.
5. Tiên đề 5 (tiên đề hóa rắn)
Một vật biến dạng cân bằng dưới tác dụng của một hệ lực thì khi hóa rắn nó vẫn cân bằng.
Chú ý: điều ngược lại không đúng
6. Tiên đề 6 (tiên đề về giải phóng liên kết)
Vật rắn chịu liên kết cân bằng có thể được xem là vật rắn tự do cân bằng nếu ta thay các liên kết bằng các phản lực liên kết (Hình 1.16).
Chú ý về liên kết thanh: trong trường hợp giữa 2 vật rắn được nối với nhau bởi 1 thanh cứng, nếu bỏ qua trọng lượng thanh có thể xem là liên kết thanh với phản lực liên kết là một lực có phương dọc theo đường thẳng nối giữa hai đầu thanh (Hình 1.17) nhờ vào tiên đề 1.
\( \left( {{\overrightarrow{F}}_{1}},{{\overrightarrow{F}}_{2}},…,{{\overrightarrow{F}}_{n}},thanh\text{ }AB,thanh\text{ }CD \right)\sim \left( {{\overrightarrow{F}}_{1}},{{\overrightarrow{F}}_{2}},…,{{\overrightarrow{F}}_{n}},{{\overrightarrow{S}}_{1}},{{\overrightarrow{S}}_{2}} \right) \)
