Thư Viện Bài Giảng Vật Lý Đại Cương
1.1. Các khái niệm cơ bản
Yêu cầu:
(1) Hiểu được các khái niệm cơ bản của cơ học: Vật rắn tuyệt đối, cân bằng lực, liên kết và phản lực liên kết.
(2) Nắm được các liên kết thường gặp và vẽ được phản lực liên kết của nó.
(3) Nắm được hệ tiên đề tĩnh học
1. Vật rắn tuyệt đối
Vật rắn tuyệt đối là một tập hợp vô hạn các chất điểm mà khoảng cách giữa 2 chất điểm bất kỳ luôn luôn không thay đổi.
– Vật rắn tuyệt đối là mô hình đơn giản nhất của vật thể.
– Trong nhiều trường hợp, khi nghiên cứu vật thể có thể coi là vật rắn tuyệt đối: ví dụ vật thể có biến dạng nhỏ,…
– Trong toàn bộ phần I này, mô hình vật thể là vật rắn tuyệt đối và ta gọi tắt là vật rắn.
Nhận Dạy Kèm môn Cơ Học Kỹ Thuật (Cơ học cơ sở) - Engineering Mechanics Online qua ứng dụng Zoom, Google Meet,...
- Dạy kèm online tương tác 1 thầy 1 trò! Hỗ trợ trực tuyến 24/7
- Dạy kèm Vật Lý Kỹ Thuật gồm:
- Cơ Học Kỹ Thuật (Cơ Học Cơ Sở) - Engineering Mechanics
- Sức Bền Vật Liệu - Mechanics of Materials
- Cơ Lưu Chất - Fluid Mechanics
- Sách Giải Bài Tập của các bộ Vật Lý Đại Cương - Vật Lý Đại Cương - Vật Lý Lý Thuyết
- Bồi dưỡng ôn thi HSG các cấp - Luyện Thi vào lớp 10 khối Chuyên, Ôn Thi Đại Học môn Vật lý
- Lịch học sắp xếp sáng - chiều - tối, tất cả các buổi từ thứ 2 ➜ CN
- Thời lượng học 1,5h - 2h/1 buổi!
2. Cân bằng
Cân bằng là trạng thái đứng yên của vật thể so với một vật thể khác được chọn làm mốc. Vật thể làm mốc được gọi là hệ quy chiếu. Trong tĩnh học, hệ quy chiếu được chọn phải thỏa mãn định luật quán tính của Newton (hệ quy chiếu đứng yên tuyệt đối). Cân bằng khi đó được gọi là cân bằng tuyệt đối.
3. Lực
Lực là một đại lượng vật lý hiển thị sự tương tác giữa các vật mà kết quả là thay đổi trạng thái cơ bản của vật. Lực được đặc trưng bởi các yếu tố:
+ Điểm đặt lực: Vị trí các vật tương tác.
+ Phương chiều lực: Phương chiều của tương tác.
+ Cường độ lực: Độ lớn này đo bằng đơn vị lực gọi là Newton, ký hiệu là N, cũng như các bội số của nó: KiloNewton (kN), …

Mô hình toán học của lực là vectơ lực, là đại lượng vectơ, ví dụ lực \( \overrightarrow{F} \), … Phương chiều và độ lớn của vectơ biểu diễn phương chiều và cường độ lực. Đường thẳng chứa vectơ lực gọi là đường tác dụng của lực (Hình 1.1)
4. Hệ lực
Hệ lực là một tập hợp nhiều lực tác dụng lên một vật. Ký hiệu hệ lực: \( \varphi \left( {{\overrightarrow{F}}_{1}},{{\overrightarrow{F}}_{2}},…,{{\overrightarrow{F}}_{n}} \right) \) (Hình 1.2)

Hai hệ lực được gọi là tương đương nếu chúng gây ra cho cùng một vật rắn các trạng thái cơ học như nhau: \( \varphi \left( {{\overrightarrow{F}}_{1}},{{\overrightarrow{F}}_{2}},…,{{\overrightarrow{F}}_{n}} \right)\simeq \phi \left( {{\overrightarrow{\Phi }}_{1}},{{\overrightarrow{\Phi }}_{2}},…,{{\overrightarrow{\Phi }}_{n}} \right) \) (Hình 1.3)
Hệ lực cân bằng là hệ lực mà dưới tác dụng của nó vật rắn ở trạng thái cân bằng hay nói cách khác hệ lực cân bằng là hệ lực có hợp lực bằng 0.
\( \varphi \left( {{\overrightarrow{F}}_{1}},{{\overrightarrow{F}}_{2}},…,{{\overrightarrow{F}}_{n}} \right)\simeq 0 \)
5. Ngẫu lực
Ngẫu lực là hệ gồm 2 lực song song ngược chiều và có cùng cường độ.
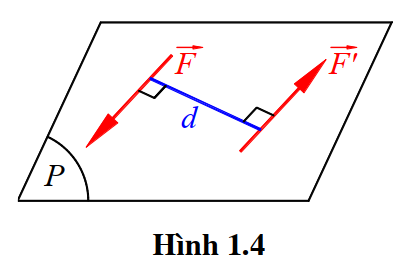
a) Một ngẫu lực được đặc trưng bởi các yếu tố sau:
– Mặt phẳng tác dụng của ngẫu lực là mặt phẳng P chứa các lực của ngẫu lực.
– Chiều quay của ngẫu lực nằm trong mặt phẳng P.
– Cường độ của ngẫu lực tỉ lệ thuận với cường độ của lực cũng như khoảng cách hai lực d gọi là cánh tay đòn của ngẫu, như vậy nó được đặc trưng bằng tích \( F.d \) gọi là giá trị moment của ngẫu. Đơn vị đo moment ngẫu lực là Newton mét (N.m) và các bội số của nó: kN.m, …
b) Trong không gian, khi các ngẫu lực nằm trong các mặt phẳng khác nhau, ngẫu lực được biểu diễn bằng vectơ moment ngẫu lực, ký hiệu \( \overrightarrow{m} \) được xác định như sau (Hình 1.5):

– Phương vuông góc với mặt phẳng chứa ngẫu lực.
– Chiều: đứng theo chiều đó thấy ngẫu lực quay ngược chiều kim đồng hồ.
– Độ lớn m được xác định bằng giá trị moment ngẫu lực là \( F.d \).
Quy ước gốc của vectơ \( \overrightarrow{m} \) nằm trên mặt phẳng chứa ngẫu lực. Trong trường hợp tất cả các ngẫu lực nằm trong mặt phẳng, khi đó nếu biểu diễn bằng vectơ moment ngẫu chúng đều song song với nhau, vì vậy, trong trường hợp này, ta chỉ cần dùng momen đại số để biểu diễn ngẫu, ký hiệu \( m=\pm Fd \), lấy dấu (+) khi quay ngược chiều kim đồng hồ, lấy dấu (-) khi quay ngược lại.
6. Liên kết và phản lực liên kết
Liên kết là những điều kiện cản trở di chuyển của vật. Trong tĩnh học sự cản trở này được thực hiện bằng việc tiếp xúc giữa các vật. Vật bị cản trở gọi là vật không tự do.
Trong các bài toán tĩnh học, vật rắn được ta chọn nghiên cứu gọi là vật khảo sát, các vật rắn khác gây cản trở di chuyển vật khảo sát gọi là vật gây liên kết, lực tạo ra do vật gây liên kết tác động lên vật khảo sát gọi là phản lực liên kết.
Phản lực liên kết luôn có chiều ngược với chiều vật khảo sát muốn di chuyển khi bị cản trở bởi vật gây liên kết.
Các loại liên kết thường gặp:
a) Liên kết tựa
Vật tựa lên mặt, chuyển động của vật bị cản trở theo phương pháp tuyến với mặt tựa, do đó, phản lực liên kết tựa luôn có phương pháp tuyến chung giữa 2 mặt tiếp xúc và đi ra khỏi mặt tựa (Hình 1.6)

Chú ý:
– Trong trường hợp một trong 2 mặt phẳng tiếp xúc là một điểm thì phản lực liên kết hướng theo pháp tuyến mặt còn lại (Hình 1.6b)
– Gối tựa di động là 1 dạng của liên kết tựa (Hình 1.6c)
b) Liên kết dây mềm

Liên kết dây mềm xuất hiện khi dây mềm không dãn, bị kéo căng. Phản lực liên kết gọi là lực căng dây có phương dọc dây và đi ra khỏi vật khảo sat, thường ký hiệu là \( \overrightarrow{T} \) (Hình 1.7)
c) Liên kết bản lề trụ

Bản lề trụ gồm một lõi trụ tròn gọi là trục bản lề và một vỏ trụ bao ngoài lõi trụ tròn đó. Lõi trụ gắn với vật khảo sát còn vỏ trụ gắn vào vật gây liên kết (Hình 1.8).
Chuyển động của vật khảo sát không bị cản trở theo hướng dọc trục, do đó phản lực liên kết bản lề trụ có phương bất kỳ vuông góc với trục bản lề, ký hiệu \( {{\overrightarrow{R}}_{A}} \). Thường để thuận tiện ta phân \( {{\overrightarrow{R}}_{A}} \) ra thành 2 thành phần theo các trục Ax và Ay là 2 trục tọa độ Descartes vuông góc nằm trong mặt phẳng vuông góc với trục bản lề \( {{\overrightarrow{R}}_{A}}\equiv \left( {{\overrightarrow{X}}_{A}},{{\overrightarrow{Y}}_{A}} \right) \) (Hình 1.8b). Gối tựa cố định là một dạng của liên kết bản lề trụ (Hình 1.8c).
d) Liên kết bản lề cầu

Vật khảo sát được gắn vào một quả cầu xoay tự do trong mặt hốc cầu. Vì liên kết này cản trở vật di chuyển theo mọi phía đối với tâm quả cầu nên phản lực liên kết bản lề cầu \( \overrightarrow{R} \) là một lực đặt tại tâm quả cầu và có phương tùy ý trong không gian. Người ta cũng thường phân \( \overrightarrow{R} \) ra 3 thành phần theo 3 trục tọa độ Descartes vuông góc với các gốc là tâm quả cầu \( {{\overrightarrow{R}}_{A}}\equiv \left( {{\overrightarrow{X}}_{A}},{{\overrightarrow{Y}}_{A}},{{\overrightarrow{Z}}_{A}} \right) \) (Hình 1.9a). Liên kết cối trụ (Hình 1.9b) cũng thuộc dạng bản lề cầu, chỉ lưu ý phản lực \( \overrightarrow{R} \) có phương bất kỳ nhưng hướng lên phía trên so với đáy cối.
e) Liên kết ngàm

Vật khảo sát và vật gây liên kết được gắn cứng vào nhau được gọi là là liên kết ngàm.
Ví dụ: dầm gắn cứng vào tường, đinh đóng chặt vào tường, … trong trường hợp này vật gây liên kết cản trở cả dịch chuyển dài lẫn dịch chuyển xoay quanh điểm gắn. Do vậy, phản lực liên kết ngàm là một lực \( \overrightarrow{R} \) có phương bất kỳ và một ngẫu lực xác định bởi moment ngẫu \( \overrightarrow{\mathcal{M}} \) có phương bất kỳ \( \left( \overrightarrow{R},\overrightarrow{\mathcal{M}} \right)\simeq \left( {{\overrightarrow{X}}_{A}},{{\overrightarrow{Y}}_{A}},{{\overrightarrow{Z}}_{A}},{{\mathcal{M}}_{x}},{{\mathcal{M}}_{y}},{{\mathcal{M}}_{z}} \right) \) (Hình 1.10a).
Nếu ngàm trong mặt phẳng, gọi tắt là ngàm phẳng thì \( \overrightarrow{R} \) chỉ có 2 thành phần \( {{\overrightarrow{X}}_{A}},{{\overrightarrow{Y}}_{A}} \) và moment ngẫu đại số \( \mathcal{M} \) (Hình 1.10b). \( \left( \overrightarrow{R},\overrightarrow{\mathcal{M}} \right)\simeq \left( {{\overrightarrow{X}}_{A}},{{\overrightarrow{Y}}_{A}},\mathcal{M} \right) \)
Các bài viết cùng chủ đề!
Các Sách Giải Bài Tập - Đề Thi do Trung tâm phát hành!
Thư Viện Bài Giảng Vật Lý Đại Cương được xây dựng trên WordPress









