Thư Viện Bài Giảng Vật Lý Đại Cương

a) Vectơ moment của lực đối với 1 điểm

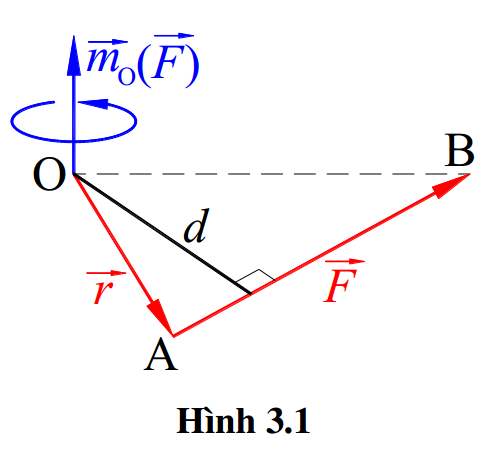
Vectơ moment của lực  \( \overrightarrow{F} \) đối với điểm O, được kí hiệu  \( {{\vec{m}}_{O}}(\overrightarrow{F}) \) là vectơ có (Hình 3.1):

– Phương: vuông góc với mặt phẳng qua O và chứa  \( \overrightarrow{F} \).

– Chiều: nhìn từ đầu mút xuống thấy  \( \overrightarrow{F} \) quay ngược chiều kim đồng hồ quanh O.

– Trị số:  \( F\cdot d \) (với d là cánh tay đòn, là khoảng cách từ O đến đường tác dụng của  \( \overrightarrow{F} \)).

+ Nhận xét:

– Trị số của vectơ moment lực  \( \overrightarrow{F} \) đối với điểm O bằng 2 lần diện tích tam giác OAB.

– Nếu đưa vào vectơ  \( \overrightarrow{OA}=\vec{r} \) là vectơ định vị điểm đặt lực  \( \overrightarrow{F} \) đối với O thì ta có:  \( {{\vec{m}}_{O}}(\overrightarrow{F})=\vec{r}\times \overrightarrow{F}\,\,\,\,\,\,\,(3.2) \)

b) Moment của lực đối với 1 trục

Moment của lực  \( \overrightarrow{F} \) đối với trục  \( \Delta \) , kí hiệu  \( {{\tilde{m}}_{\Delta }}(\overrightarrow{F}) \) là moment đại số của lực  \( \overrightarrow{{{F}’}} \) đối với điểm O, trong đó  \( \overrightarrow{{{F}’}} \) là hình chiếu của  \( \overrightarrow{F} \) lên mặt phẳng  \( \pi  \) vuông góc với trục  \( \Delta \) , còn O là giao điểm của  \( \pi  \) với trục  \( \Delta \)  (Hình 3.2).

 \( {{\tilde{m}}_{\Delta }}(\overrightarrow{F})={{\tilde{m}}_{O}}(\overrightarrow{{{F}’}})=\pm {F}’\cdot {d}’\,\,\,\,\,\,\,\,\,\,(3.3) \)

Nhận xét: Khi  \( \overrightarrow{F} \) cắt hay song song với trục  \( \Delta \)  ( \( \overrightarrow{F} \) và  \( \Delta  \) đồng phẳng) thì:  \( {{\tilde{m}}_{\Delta }}(\overrightarrow{F})=0 \).

c) Định lí liên hệ giữa moment của lực đối với một điểm và với 1 trục

Định lí: Moment của lực  \( \overrightarrow{F} \) đối với trục  \( \Delta  \) bằng hình chiếu lên trục ấy của vectơ moment của lực  \( \overrightarrow{F} \) đối với điểm O nằm trên  \( \Delta \) .

 \( {{\tilde{m}}_{\Delta }}(\overrightarrow{F})=h{{c}_{\Delta }}{{\tilde{m}}_{O}}(\overrightarrow{F})\,\,\,\,\,\,\,\,\,\,(3.4) \), với  \( O\in \Delta  \)

Chứng minh:

Chọn trục z trùng với trục  \( \Delta  \) và mặt phẳng tọa độ Oxy trùng với mặt phẳng  \( \pi \).

Gọi  \( {A}’ \) là hình chiếu của điểm đặt A của lực  \( \overrightarrow{F} \) trên mặt phẳng Oxy. Nếu A có các tọa độ (x,y,z) thì  \( {A}’ \) có các tọa độ là (x,y,0).

Từ định nghĩa moment của lực đối với một trục đối với một trục, ta có:

 \( {{\tilde{m}}_{\Delta }}(\overrightarrow{F})={{\vec{m}}_{O}}(\overrightarrow{{{F}’}})=h{{c}_{Oz}}\left[ {{{\vec{m}}}_{O}}(\overrightarrow{{{F}’}}) \right]\,\,\,\,\,\,\,(1) \)

Dựa vào biểu thức vectơ moment của lực đối với một điểm, ta viết:

 \( {{\vec{m}}_{O}}(\overrightarrow{{{F}’}})=\vec{\rho }\wedge \overrightarrow{{{F}’}}=\left[ \begin{matrix}   \overrightarrow{i} & \overrightarrow{j} & {\vec{k}}  \\   x & y & 0  \\   {{F}_{x}} & {{F}_{y}} & 0  \\\end{matrix} \right] \), trong đó:  \( \vec{\rho }=\overrightarrow{O{A}’} \).

Từ đó ta dễ dàng tính được:  \( h{{c}_{Oz}}\left[ {{{\vec{m}}}_{O}}(\overrightarrow{{{F}’}}) \right]=x{{F}_{y}}-y{{F}_{x}} \).

Mà  \( h{{c}_{Oz}}\left[ {{{\vec{m}}}_{O}}(\overrightarrow{F}) \right]=x{{F}_{y}}-y{{F}_{x}} \) nên  \( h{{c}_{Oz}}\left[ {{{\vec{m}}}_{O}}(\overrightarrow{{{F}’}}) \right]=h{{c}_{Oz}}\left[ {{{\vec{m}}}_{O}}(\overrightarrow{F}) \right]\,\,\,\,\,\,\,\,\,\,\,(2) \)

Từ (1) và (2), ta có:  \( {{\tilde{m}}_{\Delta }}(\overrightarrow{F})=h{{c}_{Oz}}\left[ {{{\vec{m}}}_{O}}(\overrightarrow{{{F}’}}) \right]=h{{c}_{Oz}}\left[ {{{\vec{m}}}_{O}}(\overrightarrow{F}) \right] \) (đpcm)

d) Vectơ moment chính của hệ lực không gian đối với điểm O

Kí hiệu  \( \overrightarrow{{{\mathcal{M}}_{O}}} \) là một vectơ bằng tổng hình học các vectơ moment của các lực lấy với điểm O đó.

 \( \overrightarrow{{{\mathcal{M}}_{O}}}=\sum\limits_{k=1}^{n}{{{{\vec{m}}}_{O}}(\overrightarrow{{{F}_{k}}})}\,\,\,\,\,\,\,\,\,\,(3.5) \)