Thư Viện Bài Giảng Vật Lý Đại Cương

a) Phương trình chuyển động

Chuyển động của chất điểm là sự thay đổi vị trí của nó theo thời gian so với một vật chuẩn gọi là hệ quy chiếu. Quy luật thay đổi này gọi là phương trình chuyển động của điểm.

+ Phương trình chuyển động dạng vectơ:

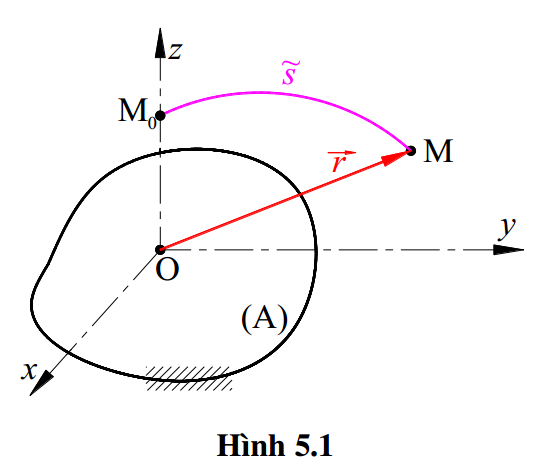
Xét chuyển động của chất điểm M đối với hệ quy chiếu (A), vị trí của nó dx xác định bằng vectơ  \( \vec{r}=\overrightarrow{OM} \) gọi là vectơ định vị của điểm M. Khi M di chuyển, vectơ  \( \vec{r} \) thay đổi theo thời gian:  \( \vec{r}=\vec{r}(t)\,\,\,\,\,\,\,\,(5.1) \)

(5.1) được gọi là phương trình chuyển động của chất điểm M dạng vectơ. Đường cong do M vạch ra trong không gian khi nó chuyển động gọi là quỹ đạo chuyển động của chất điểm M.

+ Phương trình chuyển động dạng tọa độ Descartes

Nếu tại điểm  \( O\in (A) \), ta lập hệ tọa độ Descartes vuông góc Oxyz. Điểm M có 3 tọa độ (x,y,z). Khi M chuyển động, ta có:  \( \left\{ \begin{align}  & x=x(t) \\  & y=y(t) \\  & z=z(t) \\ \end{align} \right.\,\,\,\,\,\,\,\,(5.2) \)

(5.2) gọi là phương trình chuyển động của M dạng tọa độ Descartes.

Chú ý:  \( \vec{r}=x\cdot \overrightarrow{i}+y\cdot \overrightarrow{j}+z\cdot \vec{k}\,\,\,\,\,\,\,(5.3) \), trong đó:  \( \overrightarrow{i},\overrightarrow{j},\vec{k} \) là các vectơ chỉ phương của các trục Ox, Oy, Oz.

+ Phương trình chuyển động dạng tọa độ tự nhiên

Sử dụng trong trường hợp biết trước quỹ đạo chuyển động. Trên quỹ đạo chuyển động, chọn điểm M₀ cố định làm gốc và quy định chiều dương quỹ đạo. Khi đó vị trí của điểm M trên quỹ đạo được xác định bởi cung đường cong  \( s=OM \). Khi M chuyển động, s sẽ là hàm của thời gian t.

 \( s=s(t)\,\,\,\,\,\,\,\,\,\,\,\,(5.4) \)

(5.4) gọi là phương trình chuyển động của điểm M dạng tọa độ tự nhiên.

b) Vận tốc và gia tốc

+ Vận tốc và gia tốc dạng vectơ

Vận tốc của điểm M chuyển động là đại lượng biểu diễn nhịp độ thay đổi nhanh hay chậm của động điểm M, nó là đại lượng vectơ.

Giả sử: tại thời điểm t, M được xác định bởi vectơ định vị  \( \vec{r}(t) \); tại thời điểm  \( t+\Delta t \), M được xác định bởi vectơ định vị  \( \vec{r}(t+\Delta t) \).

Như vậy, sau khoảng thời gian  \( \Delta t \), vectơ định vị thay đổi một lượng:  \( \Delta \vec{r}=\vec{r}(t+\Delta t)-\vec{r}(t) \).

Ta gọi là  \( {{\vec{v}}_{tb}}=\frac{\Delta \vec{r}}{\Delta t} \) là vận tốc trung bình của điểm M trong khoảng thời gian  \( \Delta t \). Vận tốc của điểm M tại thời điểm t:  \( {{\vec{v}}_{tb}}=\underset{\Delta t\to 0}{\mathop{\lim }}\,\frac{\Delta \vec{r}}{\Delta t}=\frac{d\vec{r}}{dt}=\dot{\vec{r}}\,\,\,\,\,\,\,\,(5.5) \)

Vậy, vectơ vận tốc của động điểm được tính bằng đạo hàm bậc I của vectơ định vị theo thời gian.

Vectơ vận tốc có phương tiếp tuyến với quỹ đạo tại điểm M và có chiều về phía chuyển động của điểm M (Hình 5.2).

Đơn vị của vận tốc là mét/giây, kí hiệu m/s.

Gia tốc của điểm M chuyển động là đại lượng biểu thị nhịp độ nhanh hay chậm của vận tốc của nó. Gia tốc là đại lượng vectơ.

Giả sử: tại thời điểm t, động điểm M có vận tốc  \( \vec{v}(t) \), sau thời gian  \( \Delta t \), nó có vận tốc  \( \vec{v}(t+\Delta t) \).

Gọi  \( {{\vec{a}}_{tb}}=\frac{\Delta \vec{a}}{\Delta t}=\frac{\vec{v}(t+\Delta t)-\vec{v}(t)}{\Delta t} \) là gia tốc trung bình của động điểm trong khoảng thời gian  \( \Delta t \).

Gia tốc của điểm M tại thời điểm t:  \( {{\vec{a}}_{tb}}=\underset{\Delta t\to 0}{\mathop{\lim }}\,\frac{\Delta \vec{v}}{\Delta t}=\frac{d\vec{v}}{dt}=\frac{{{d}^{2}}\vec{r}}{d{{t}^{2}}}=\ddot{\vec{r}}\,\,\,\,\,\,\,\,(5.6) \)

Vậy, gia tốc của động điểm bằng đạo hàm bậc I của vận tốc theo thời gian hoặc bằng đạo hàm bậc II theo thời gian của vectơ định vị.

Đơn vị của gia tốc là mét/giây², kí hiệu m/s².

Động điểm là chuyển động nhanh dần hay chậm dần nếu ta biết  \( \vec{v} \) và  \( \vec{a} \) tại thời điểm t. Chuyển động của động điểm gọi là nhanh dần (hoặc chậm dần) nếu  \( \left| {\vec{v}} \right| \) hoặc tương đương với nó  \( \frac{1}{2}{{v}^{2}} \) tăng (hoặc giảm) theo thời gian.

Vậy  \( \frac{d}{dt}\left( \frac{1}{2}{{v}^{2}} \right)=\frac{d}{dt}\left( \frac{1}{2}{{{\vec{v}}}^{2}} \right)=\vec{v}\cdot \vec{a}\,\,\,\,\left\{ \begin{align}  & >0:\text{nhanh dn} \\  & <0:\text{ ch }\!\!\ddot{\mathrm{E}}\!\!\text{ m dn} \\ \end{align} \right.\,\,\,\,\,\,\,(5.7) \)

+ Vận tốc và gia tốc dạng tọa độ Descartes

Ta biết:  \( \vec{v}=\frac{d\vec{r}}{dt}=\frac{d}{dt}\left( x\cdot \overrightarrow{i}+y\cdot \overrightarrow{j}+z\cdot \vec{k} \right)=\dot{x}\cdot \overrightarrow{i}+\dot{y}\cdot \overrightarrow{j}+\dot{z}\cdot \vec{k} \)

Chiếu 2 vế lên các trục tọa độ Ox, Oy, Oz, ta được:  \( {{v}_{x}}=\dot{x};\,\,{{v}_{y}}=\dot{y};\,\,{{v}_{z}}=\dot{z}\,\,\,\,\,\,\,\,\,\,\,\,(5.8) \)

Từ (5.8), ta tính được:  \( v=\left| {\vec{v}} \right|=\sqrt{v_{x}^{2}+v_{y}^{2}+v_{z}^{2}}=\sqrt{{{{\dot{x}}}^{2}}+{{{\dot{y}}}^{2}}+{{{\dot{z}}}^{2}}}\,\,\,\,\,\,\,\,\,\,\,\,\,(5.9) \)

 \( \cos \left( \vec{v},Ox \right)=\frac{{{v}_{x}}}{v};\,\,\cos \left( \vec{v},Oy \right)=\frac{{{v}_{y}}}{v};\,\,\cos \left( \vec{v},Oz \right)=\frac{{{v}_{z}}}{v}\,\,\,\,\,\,\,\,\,\,\,\,(5.10) \)

Ta có:  \( \vec{a}=\frac{d\vec{v}}{dt}=\frac{d}{dt}\left( \dot{x}\cdot \overrightarrow{i}+\dot{y}\cdot \overrightarrow{j}+\dot{z}\cdot \vec{k} \right)=\ddot{x}\cdot \overrightarrow{i}+\ddot{y}\cdot \overrightarrow{j}+\ddot{z}\cdot \vec{k} \)

Chiếu 2 vế lên các trục tọa độ, ta được:  \( {{\vec{a}}_{x}}=\ddot{x};\,\,{{\vec{a}}_{y}}=\ddot{y};\,\,{{\vec{a}}_{z}}=\ddot{z}\,\,\,\,\,\,\,\,\,\,\,(5.11) \)

Từ (5.11), ta tính được:  \( a=\left| {\vec{a}} \right|=\sqrt{a_{x}^{2}+a_{y}^{2}+a_{z}^{2}}=\sqrt{{{{\ddot{x}}}^{2}}+{{{\ddot{y}}}^{2}}+{{{\ddot{z}}}^{2}}}\,\,\,\,\,\,\,\,\,\,(5.12) \)

 \( \cos \left( \vec{a},Ox \right)=\frac{{{a}_{x}}}{a};\,\,\cos \left( \vec{a},Oy \right)=\frac{{{a}_{y}}}{a};\,\,\cos \left( \vec{a},Oz \right)=\frac{{{a}_{z}}}{a}\,\,\,\,\,\,\,\,\,\,\,\,(5.13) \)

+ Vận tốc và gia tốc dạng tọa độ tự nhiên

– Hệ tọa độ tự nhiên: Tại điểm M trên đường cong quỹ đạo, ta dựng 3 trục tọa độ:

Trục  \( M\tau \)  theo phương tiếp tuyến với đường cong.

Trục Mn theo phương pháp tuyến chính của đường cong.

Trục Mb để hệ  \( M\tau nb \) tạo thành một tam diện thuận.

Trục  \( M\tau \)  gọi là trục tiếp tuyến.

Trục Mn gọi là trục pháp tuyến chính.

Trục Mb gọi là trục trùng pháp tuyến tạo thành hệ tọa độ tự nhiên.

– Xác định vận tốc trong hệ tọa độ tự nhiên

Tại thời điểm t, động điểm M được xác định bởi cung  \( s(t) \).

Tại thời điểm  \( t+\Delta t \), nó được xác định bởi cung s(t+\Delta t).

Gọi là  \( {{v}_{tb}}=\frac{\Delta s}{\Delta t}=\frac{s(t+\Delta t)-s(t)}{\Delta t} \) là vận tốc trung bình của động điểm M trong khoảng thời gian  \( \Delta t \).

Vận tốc của điểm động M tại thời điểm t là:  \( \tilde{v}=\underset{\Delta t\to 0}{\mathop{\lim }}\,\frac{\Delta s}{\Delta t}=\frac{ds(t)}{dt}=\dot{s}(t)\,\,\,\,\,\,\,\,\,\,(5.14) \)

Ta đã biết phương vectơ  \( \vec{v} \) là theo tiếp tuyến với quỹ đạo, tức theo phương  \( M\tau  \):

Nếu  \( \Delta s>0\to v>0 \) thì vectơ  \( \vec{v} \) hướng theo chiều dương trục M\tau .

Nếu  \( \Delta s<0\to v<0 \) thì vectơ  \( \vec{v} \) hướng theo chiều ngược lại.

– Xác định gia tốc trong hệ tọa độ tự nhiên:

Ta có:  \( \vec{a}=\frac{d\vec{v}}{dt}=\frac{d(v\cdot {{{\vec{\tau }}}_{0}})}{dt}=\frac{dv}{dt}\cdot {{\vec{\tau }}_{0}}+v\cdot \frac{d{{{\vec{\tau }}}_{0}}}{dt} \).

Chú ý:  \( \frac{d{{{\vec{\tau }}}_{0}}}{dt}=\frac{d{{{\vec{\tau }}}_{0}}}{ds}\cdot \frac{ds}{dt}=\frac{d{{{\vec{\tau }}}_{0}}}{dt}\cdot v \).

Mặt khác, theo lý thuyết về vectơ, ta có:  \( \frac{d{{{\vec{\tau }}}_{0}}}{ds}=k\cdot {{\vec{n}}_{0}} \), với k là độ cong của đường cong và  \( k=\frac{1}{\rho } \); với   \( \rho  \) là bán kính cong của đường cong quỹ đạo tại điểm M.

Vậy  \( \frac{d{{{\vec{\tau }}}_{0}}}{dt}=\frac{v}{\rho }\cdot {{\vec{n}}_{0}} \).

Từ đó suy ra:  \( \vec{a}=\frac{dv}{dt}\cdot {{\vec{\tau }}_{0}}+v\cdot \frac{d{{{\vec{\tau }}}_{0}}}{dt}=\frac{dv}{dt}\cdot {{\vec{\tau }}_{0}}+v\cdot \frac{v}{\rho }\cdot {{\vec{n}}_{0}} \) hay  \( \vec{a}=\frac{dv}{dt}\cdot {{\vec{\tau }}_{0}}+\frac{{{v}^{2}}}{\rho }\cdot {{\vec{n}}_{0}}={{\vec{a}}_{\tau }}+{{\vec{a}}_{n}}\,\,\,\,\,\,\,\,\,\,\,\,\,\,(5.15) \)

Chiếu  \( \vec{a} \) lên hệ trục  \( M\tau nb \), ta được:

 \( {{a}_{\tau }}=\frac{dv}{dt}=\dot{v} \) gọi là thành phần gia tốc tiếp tuyến.

 \( {{a}_{n}}=\frac{{{v}^{2}}}{\rho } \) gọi là thành phần gia tốc pháp tuyến.

 \( {{\vec{a}}_{\tau }}=\dot{v}\cdot {{\vec{\tau }}_{0}} \) được gọi là gia tốc tiếp tuyến; còn  \( {{\vec{a}}_{n}}=\frac{{{v}^{2}}}{\rho }{{\vec{n}}_{0}} \) được gọi là gia tốc pháp tuyến. Gia tốc pháp tuyến luôn hướng theo chiều dương của trục pháp tuyến chính (tức luôn hướng theo phía lõm của đường cong quỹ đạo) (Hình 5.5).

 \( a=\sqrt{a_{\tau }^{2}+a_{n}^{2}}=\sqrt{{{{\dot{v}}}^{2}}+\frac{{{v}^{4}}}{{{\rho }^{2}}}}\,\,\,\,\,\,\,\,\,\,\,(5.16) \)

 \( \tan \alpha =\frac{{{a}_{\tau }}}{{{a}_{n}}}=\frac{\dot{v}\cdot \rho }{{{v}^{2}}}\,\,\,\,\,\,\,\,\,\,\,(5.17) \)

Ta nhận thấy:

Gia tốc tiếp tuyến đặc trưng cho sự biến thiên về giá trị của vận tốc.

Gia tốc pháp tuyến đặc trưng cho sự biến thiên về phương của vectơ vận tốc.

Chú ý: Khi quỹ đạo là đường tròn bán kính R thì bán kính cong của quỹ đạo  \( \rho =R;\,\,{{a}_{n}}=\frac{{{v}^{2}}}{R} \).

c) Những chuyển động đặc biệt

+ Chuyển động thẳng:

Chuyển động thẳng là chuyển động có quỹ đạo là một đường thẳng. Có 2 dạng chuyển động thường gặp:

– Chuyển động thẳng đều:  \( \vec{v}=\overrightarrow{const} \). Khi đó:  \( s={{s}_{0}}+vt\,\,\,\,\,\,\,\,\,\,\,\,(5.18) \), trong đó  \( {{s}_{0}} \) là tọa độ ban đầu ( \( t=0 \)).

– Chuyển động thẳng biến đổi đều:  \( \vec{a}=\overrightarrow{const} \). Khi đó: \(\left\{ \begin{align} & v={{v}_{0}}+a\cdot t \\ & s=\int{vdt}={{s}_{0}}+{{v}_{0}}\cdot t+a\cdot \frac{{{t}^{2}}}{2} \\ \end{align} \right.\,\,\,\,\,\,\,\,\,\,\,(5.19)\)

+ Chuyển động cong phẳng

Động điểm có quỹ đạo là đường cong phẳng. Có 2 dạng thường gặp:

– Chuyển động cong đều:  \( v=const \). Khi đó:  \( s={{s}_{0}}+vt\,\,\,\,\,\,\,\,\,\,\,\,\,\,(5.20) \)

– Chuyển động cong biến đổi đều:  \( {{a}_{\tau }}=const \). Khi đó: \(\left\{ \begin{align}  & v={{v}_{0}}+a\cdot t \\  & s=\int{vdt}={{s}_{0}}+{{v}_{0}}\cdot t+{{a}_{\tau }}\cdot \frac{{{t}^{2}}}{2} \\ \end{align} \right.\,\,\,\,\,\,\,\,\,\,\,(5.21)\)